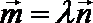- 抛物线焦点弦的性质
- 共82题
19． 已知复数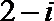
（1）求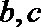
（2）若向量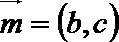
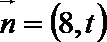
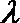
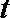
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
9． 过抛物线
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
3．点
正确答案
5
解析
解析已在路上飞奔，马上就到！
知识点
8．设
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
12．已知抛物线
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
10．已知函数
若两正数
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
2.将两个顶点在抛物线y2=2px(p>0)上,另一个顶点是此抛物线焦点的正三角形个数记为n,则( ).
正确答案
解析
如图所示,A,B两点关于x轴对称,
点F的坐标为(
则由抛物线定义,知|AF|=|AA1|,
即m+
又|AF|=|AB|=
∴m+
整理得
∴Δ=
∴方程①有两个不同的实根,
记为m1,m2,且m1+m2=7p>0,
∴m1>0,m2>0,∴n=2.
知识点
9．若抛物线y2 = 2px（p>0）上一点到焦点和抛物线的对称轴的距离分别是10和6，则p的值为（ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
20．已知椭圆形：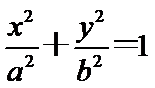
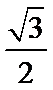
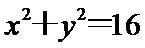
（Ⅰ）求椭圆W的方程；
（Ⅱ）若点P为椭圆W上不同于点A的点，直线AP与圆O的另一个交
正确答案
（1）
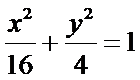
（2）不存在直线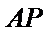
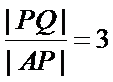
解析
解答过程如下：
（1）因为椭圆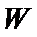
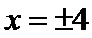
又离心率为
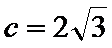
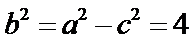
所以
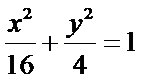
（2）设点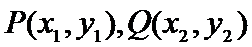
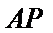
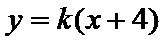
与椭圆方程联
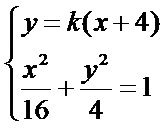
化简得到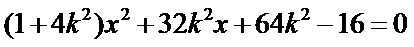
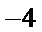
所以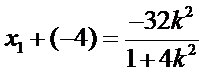
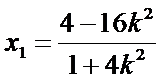
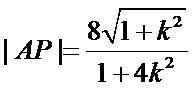
因为圆心到直线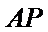
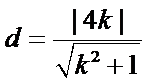
所以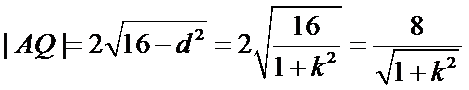
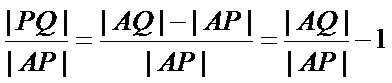
代入得到
显然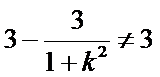
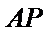
考查方向
解题思路
第（1）问根据椭圆的标准方程以及几何性质，通过待定系数的方法即可求解；
2、第（2）问可以通过直线与椭圆的位置关系建立方程组，利用韦达定理、解方程求解；
易错点
试题分析：本题第（1）问属于椭圆简单几何性质的应用，是基础知识；第（2）问是直线与椭圆的位置关系的问题，常用解析几何的基本思想方法求解，运算量比较大，需要考生在计算过程中认真、细心。
知识点
6.如果
A
B
C
D
正确答案
解析
由抛物线方程知p=2，结合焦半径公式|PF|=
考查方向
解题思路
因为|PF|=
易错点
1,由抛物线标准方程求不出P;
2、不能正确掌握抛物线的焦半径公式。
知识点
扫码查看完整答案与解析