- 由递推关系式求数列的通项公式
- 共176题
在平面直角坐标系xOy中,设定点A(a,a),P是函数

正确答案

解析
设P点的坐标为
|PA|2=

结合题意可知
(1)当a≤2,t=2时,|PA|2取得最小值,此时(2-a)2+a2-2=8,解得a=-1,a=3(舍去)。
(2)当a>2,t=a时,|PA|2取得最小值,此时a2-2=8,解得a=


知识点
已知各项均为正数的两个数列



(1)设


(2)设




正确答案
见解析
解析
(1)根据题设



(2)根据基本不等式得到


从而得到




知识点
已知{an}是由非负整数组成的无穷数列,该数列前n项的最大值记为An,第n项之后各项an+1,an+2,…的最小值记为Bn,dn=An-Bn.
(1)若{an}为2,1,4,3,2,1,4,3,…,是一个周期为4的数列(即对任意n∈N*,an+4=an),写出d1,d2,d3,d4的值;
(2)设d是非负整数,证明:dn=-d(n=1,2,3,…)的充分必要条件为{an}是公差为d的等差数列;
(3)证明:若a1=2,dn=1(n=1,2,3,…),则{an}的项只能是1或者2,且有无穷多项为1.
正确答案
见解析
解析
(1)d1=d2=1,d3=d4=3.
(2)(充分性)因为{an}是公差为d的等差数列,且d≥0,
所以a1≤a2≤…≤an≤…。
因此An=an,Bn=an+1,dn=an-an+1=-d(n=1,2,3,…)。
(必要性)因为dn=-d≤0(n=1,2,3,…),
所以An=Bn+dn≤Bn.
又因为an≤An,an+1≥Bn,所以an≤an+1.
于是,An=an,Bn=an+1,
因此an+1-an=Bn-An=-dn=d,
即{an}是公差为d的等差数列。
(3)因为a1=2,d1=1,
所以A1=a1=2,B1=A1-d1=1.
故对任意n≥1,an≥B1=1.
假设{an}(n≥2)中存在大于2的项。
设m为满足am>2的最小正整数,
则m≥2,并且对任意1≤k<m,ak≤2.
又因为a1=2,所以Am-1=2,且Am=am>2.
于是,Bm=Am-dm>2-1=1,Bm-1=min{am,Bm}≥2.
故dm-1=Am-1-Bm-1≤2-2=0,与dm-1=1矛盾。
所以对于任意n≥1,有an≤2,即非负整数列{an}的各项只能为1或2.
因为对任意n≥1,an≤2=a1,
所以An=2.
故Bn=An-dn=2-1=1.
因此对于任意正整数n,存在m满足m>n,且am=1,即数列{an}有无穷多项为1.
知识点
等差数列{an}中,a1+a5=10,a4=7,则数列{an}的公差为( )
正确答案
解析
设数列{an}的公差为d,则由a1+a5=10,a4=7,可得 2a1+4d=10,a1+3d=7,解得 d=2
知识点
已知函数
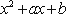
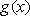

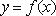
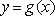
(1)求



(2)若
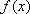
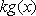

正确答案
见解析
解析
(1)由已知得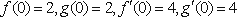
而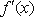
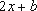
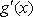
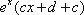




(2)由(Ⅰ)知,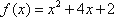
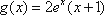
设函数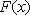

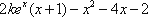

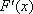
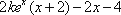
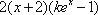
有题设可得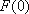

令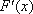
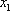
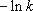

1),若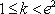
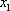
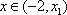
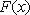
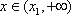
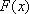
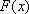
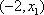
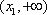
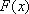

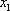
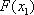
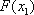
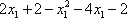
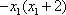
∴当
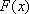
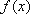
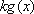
2),若

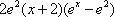
∴当
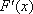
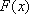

∴当
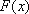
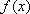
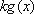
3),若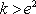
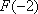
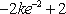
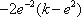
∴当
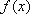
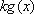
综上所述,
知识点
扫码查看完整答案与解析