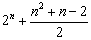· 数列的概念与简单表示法

· 由递推关系式求数列的通项公式

由递推关系式求数列的通项公式
共176题

· 数列的概念与简单表示法

· 由递推关系式求数列的通项公式

由递推关系式求数列的通项公式
共176题

热门试卷

X 查看更多试卷

1

题型：简答题

|

简答题 · 14 分

已知数列的前项和为，且满足。

（1）求，的值；

（2）求；

（3）设，数列的前项和为，求证：。

正确答案

见解析。

解析

（1）当时，有，解得。

当时，有，解得。

（2）（法一）当时，有, ………①

。 …………②

①—②得：，即：。

。

。

另解：。

又当时，有，。

（法二）根据，，猜想：。

用数学归纳法证明如下：

（1）当时，有，猜想成立。

（2）假设当时，猜想也成立，即：。

那么当时，有，

即：，①

又， …②

①-②得：，

解，得。

当时，猜想也成立。

因此，由数学归纳法证得成立，

（3），

。

知识点

由递推关系式求数列的通项公式错位相减法求和数列与不等式的综合

1

题型：简答题

|

简答题 · 18 分

已知数列满足（）。

（1）求的值；

（2）求（用含的式子表示）；

（3）记数列的前项和为，求（用含的式子表示）。

正确答案

（1）3,13,39（2）（3）

解析

（1）（），

（2）由题知，有，

。

∴，

（3） ∵，

∴。

∴。

又，

当为偶数时，

，

当为奇数时，

，

综上，有

知识点

由递推关系式求数列的通项公式分组转化法求和

1

题型：单选题

|

单选题 · 5 分

设，，为整数（m>0），若和被除得的余数相同，则称和对模同余，记为，若，，则的值可以是

A2011

B2012

C2013

D2014

正确答案

A

解析

略

知识点

由递推关系式求数列的通项公式

1

题型：填空题

|

填空题 · 5 分

已知数列满足，则（）；前2n项和（）。

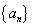
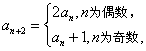
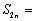
正确答案

7；

解析

略

知识点

由递推关系式求数列的通项公式分组转化法求和

1

题型：填空题

|

填空题 · 5 分

已知向量序列：满足如下条件：

，且（）。

若，则________；中第_____项最小。

正确答案

9；3

解析

略

知识点

平面向量数量积的运算由递推关系式求数列的通项公式

继续学习学习下一知识点

下一知识点 : 由其它方法求数列的通项公式

百度题库 > 高考 > 理科数学 > 由递推关系式求数列的通项公式

扫码查看完整答案与解析