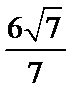- 圆的切线的性质定理的证明
- 共15题
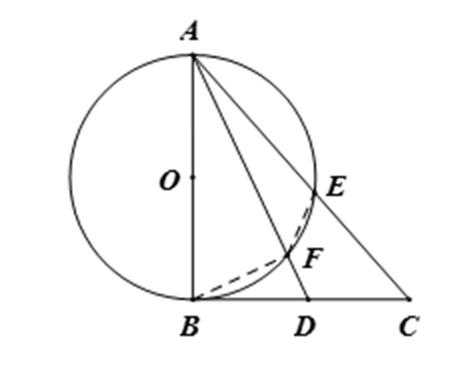
22.选修4一 1:几何证明选讲如图,直线AB为圆的切线,切点为B,点C


23.选修




24.选修4一 5 


正确答案
22(1)连接DE交BC于点G,由弦切角定理得,
∠ABE=∠BCE, ∠ABE=∠CBE,故∠CBE=∠BCE,
故BE=CE,
又因为DB垂直BE,
所以DE为直径,则∠DCE=90度,
由勾股定理可得,DB=DC
(2)由(1)知,∠CDE=∠BDE,DB=DC,
故DG是BC的中垂线,
所以
连接BO,则∠BOG=60°,从而∠ABE=∠BCE=∠CBE=30°,
所以CF⊥BF,
故Rt△BCF外接圆的半径等于 
23(1)曲线C1的普通方程为
曲线C2的普通方程为
(2)由曲线C1:

所以P点坐标为
由题意可知,M
因此,
所以当


24(1)因为函数定义域为R,所以
设函数

又

所以
故m的取值范围为
(2)由1知m=4
所以
当且仅当

7a+4b有最小值,为
解析
22无 23主要是消去参数。利用解析几何相关知识求解 24先求出函数的最小值,然后确定m的取值范围,第(2)问利用不等式的基本性质转换求解。
考查方向
22主要考查圆切线的性质,相似三角形的计算 23本题主要考查直角坐标和极坐标的相互转换,考察解析几何的简单应用 24本题主要考查不等式的性质与证明
解题思路
22利用线切角定理和勾股定理可证明第一问,第二问做出适当的辅助线即可求解 23消去参数方程中的参数即可,结合三角函数相关性质求得。24利用均值不等式、基本不等式相关性质计算
易错点
22相似度掌握不好计算能力弱 23直角坐标和极坐标不会转换 24对基本不等式掌握不牢
知识点
22.选修4-1:几何证明选讲
如图, 圆M与圆N交于A, B两点, 以A为切点作两圆的切线分别交圆M和圆N于C、D两点,延长DB交圆M于点E, 延长CB交圆N于点F.已知BC=5, DB=10.
(I)求AB的长;
(II)求
正确答案
(1)
(2)
解析
试题分析:本题属于平面几何问题,具体解析如下:
(Ⅰ)根据弦切角定理,
知

∴△


故
(Ⅱ)根据切割线定理,知

两式相除,得
由△



又
由(*)得
考查方向
本题考查了平面几何中圆幂定理的应用,大体可以分成以下几类:
1、圆与圆的位置关系;
2、弦切角定理的应用;
3、相似三角形的判定;
4、切割线定理的应用;
5、相似三角形的性质。
解题思路
本题考查平面几何内圆的相关知识,解题步骤如下:
1、根据弦切角定理判定三角形相似,进而得到AB的值;
2、根据切割线定理得到两边对应成比例,进而得出三角形相似;
3、根据三角形相似的性质,得到比例。
易错点
1、相似三角形的判定应用时条件不全;
2、切割线定理应用时两式相除这个技巧不容易想到;
3、运算出错。
知识点
22.如图,在直角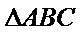

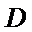

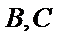
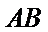

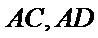
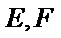
(Ⅰ)证明: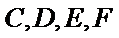
(Ⅱ)若
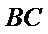
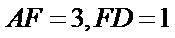
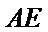
正确答案
(Ⅰ)略
(Ⅱ)
解析
试题分析:本题是有关直线与圆的问题,难度不大。在解题中注意结合切线的性质和勾股定理等知识进行解决。
(Ⅰ)连结
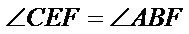
因为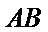
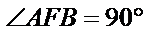
因为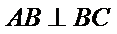

所以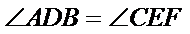
所以
(Ⅱ)由已知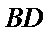

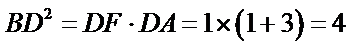
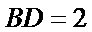
所以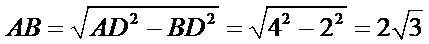
因为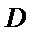
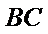
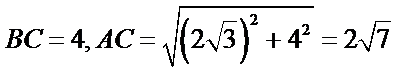
因为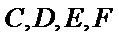
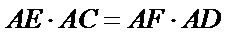
所以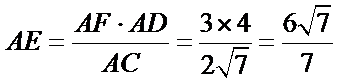
考查方向
解题思路
本题主要考查圆的基本性质、圆周角定理等基础知识。
解题步骤如下:利用四点共圆的判定定理,证明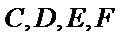
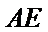
易错点
第二问计算中,不易想到利用第一问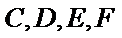
知识点
22.选修4-1:几何证明选讲
如图,已知:














(Ⅰ)求证:∠BCF=∠CAB ;
(Ⅱ)若FB=FE=1,求⊙O的半径.
正确答案
(1)略
(2)
解析
(Ⅰ)证明:因为AB是直径,
所以∠ACB=90°
又因为F是BD中点,所以∠BCF=∠CBF=90°-∠CBA=∠CAB
因此∠BCF=∠CAB
(Ⅱ)解:直线CF交直线AB于点G,
由FC=FB=FE得:∠FCE=∠FEC
可证得:

且AB=BG
由切割线定理得:(1+FG)2=BG×AG=2BG2 ……①
在Rt△BGF中,由勾股定理得:BG2=FG2-BF2 ……②
由①、②得:FG2-2FG-3=0
解之得:FG1=3,FG2=-1(舍去)
所以AB=BG=
所以⊙O半径为
考查方向
解题思路
第一问:由已知条件得FC=FB=FE得到∠BCF=∠CBF=∠CAB
第二问:由FC=FB=FE得:∠FCE=∠FEC,继而证得:

易错点
1、第一问想到弦切角定理,进而向证明CF与圆相切,虽然可以证明,但是,但是过程稍烦一些。 2、第二问没有注意题中的已知条件,而运用
知识点
11. 如下图,





则
正确答案
解析


所以
设

求得,
由勾股定理可得,

所以
所以
考查方向
解题思路
根据切线长定理,勾股定理求解
易错点
圆中线段关系弄错
知识点
扫码查看完整答案与解析