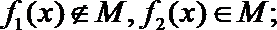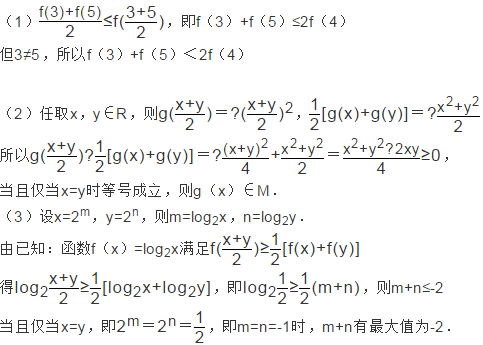- 抛物线的定义及应用
- 共187题
1
题型:填空题
|
13. 已知抛物线




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
抛物线的定义及应用
1
题型:
单选题
|
9.定义在



正确答案
D
解析
解析已在路上飞奔,马上就到!
知识点
抛物线的定义及应用
1
题型:简答题
|
22.我们将具有下列性质的所有函数组成集合M:函数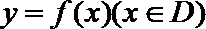
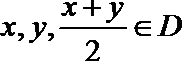

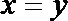
(1)若定义在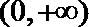
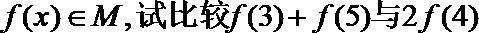
(2)给定两个函数: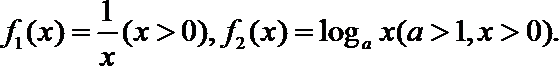
(3)试利用(2)的结论解决下列问题:若实数m,n满足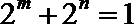
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
抛物线的定义及应用
1
题型:简答题
|
20. 已知焦点在





(1)求椭圆
(2)已知过点




① 若直线


② 若直线




正确答案
(1)设椭圆


由题意可知:

解得
∴ 椭圆

(2)由(1)得

①当直线



由

即


则直线



∵ 

∴ 
②当直线



由


因为 点


因为 


所以

∴ 





取



记点

另一方面,点

∴点

又
故

所以 当直线



解析
解析已在路上飞奔,马上就到!
知识点
抛物线的定义及应用
1
题型:填空题
|
9.已知圆C过点




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
抛物线的定义及应用
下一知识点 : 抛物线的标准方程和几何性质
扫码查看完整答案与解析