- 导数的几何意义
- 共149题
已知函数

26.若曲线



27.若



28.若


正确答案
(1)
解析
(1)当



考查方向
解题思路
1)第一问由


2)第二问由零点的概念,化简函数


3)由



易错点
求导函数,求极值,参数m的讨论是本题的易错点,
正确答案
(2)
解析
(2)由题意,

令
又
∴

∴
∴
∴
考查方向
解题思路
1)第一问由


2)第二问由零点的概念,化简函数


3)由



易错点
求导函数,求极值,参数m的讨论是本题的易错点,
正确答案
(3)综上,当





解析
(3)由

令


∴


∴
又令

令

∴


又
∴当

∴
同理,当



综上,当
当

当

考查方向
解题思路
1)第一问由


2)第二问由零点的概念,化简函数


3)由



易错点
求导函数,求极值,参数m的讨论是本题的易错点,
函数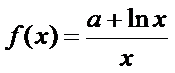
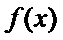

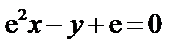
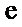

25.若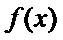
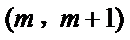


26.求证:当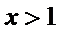
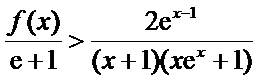
正确答案
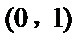
解析
因为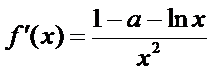
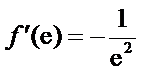
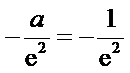
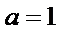
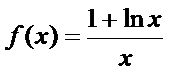
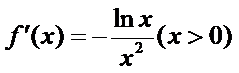
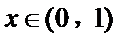
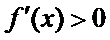
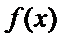
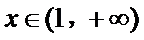
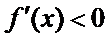
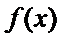
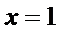
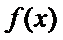
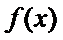
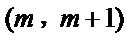
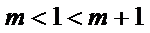
即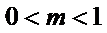
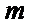
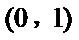
考查方向
解题思路
第一问由切线与直线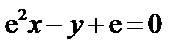
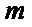
正确答案
略;
解析
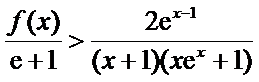
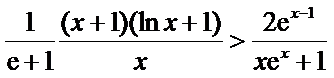
令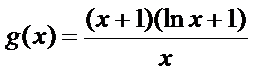
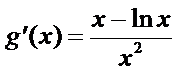
再令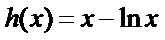
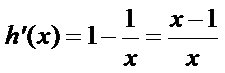
因为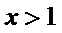
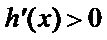
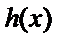
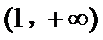
所以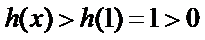
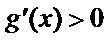
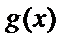
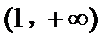
所以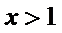
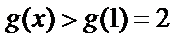

令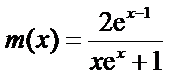

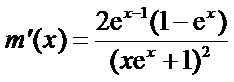
因为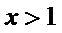
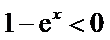
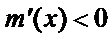
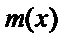
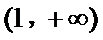
所以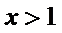
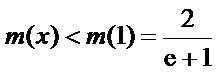
所以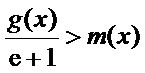
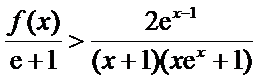
考查方向
解题思路
第二问现将不等式等级变形,构造新函数,对新函数用导函数求最值
12.已知函数





正确答案
解析


(1)当



(2)当













考查方向
解题思路
1.先求导后判断导数的正负,2.当导数有正有负时转化为一元二次方程根的分布处理,接着转化为线性规划使得问题得以解决。
易错点
1.不知道题中的条件:函数



知识点
12.已知



正确答案
解析









考查方向
解题思路
1.根据导数的几何意义求出


易错点
本题易在根据导函数的几何意义得到
知识点
10.已知





正确答案
解析
设

所以
考查方向
解题思路
1.先将函数


易错点
1.不知道将函数

知识点
扫码查看完整答案与解析




































