导数的几何意义
共149题

· 导数的几何意义

导数的几何意义
共149题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 5 分

若曲线在点处的切线与两条坐标轴围成的三角形的面积为，则___________.

正确答案

解析

求导得，所以在点处的切线方程为.令得，令得，所以切线与两条坐标轴围成的三角形的面积，（舍去负值），.

知识点

对数的运算性质导数的几何意义

题型：填空题

填空题 · 5 分

已知正数满足，，则的取值范围是______。

正确答案

解析

略

知识点

导数的几何意义

题型：填空题

填空题 · 5 分

定义在区间上的连续函数，如果，使得，则称为区间上的“中值点”，下列函数：①；②；③；④中，在区间上“中值点”多于一个的函数序号为____，（写出所有满足条件的函数的序号）

正确答案

①④

解析

略

知识点

导数的几何意义导数的运算

题型：填空题

填空题 · 4 分

已知存在实数a,满足对任意的实数b,直线y=-x+b都不是曲线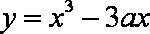的切线，则实数a的取值范围是。

正确答案

解析

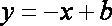
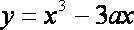
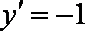
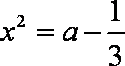
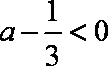
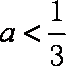
直线都不是曲线的切线,可得无解，即无解，只要，即.

知识点

导数的几何意义

题型：简答题

简答题 · 18 分

设函数定义域为，且.设点是函数图像上的任意一点，过点分别作直线和轴的垂线，垂足分别为，

（1）写出的单调递减区间（不必证明）；（4分）

（2）问：是否为定值？若是，则求出该定值，若不是，则说明理由；（7分）

（3）设为坐标原点，求四边形面积的最小值.（7分）

正确答案

见解析

解析

解析：（1）、因为函数的图象过点，

所以 2分

函数在上是减函数. 4分

（2）设 5分

直线的斜率

则的方程 6分

联立

9分

， 11分

（3） 12分

13分

∴， 14分

， 15分

∴ ， 16分

17分

当且仅当时，等号成立.

∴ 此时四边形面积有最小值.

知识点

导数的几何意义

继续学习学习下一知识点

下一知识点 : 导数的运算

百度题库 > 高考 > 理科数学 > 导数的几何意义

扫码查看完整答案与解析