- 等差数列的性质及应用
- 共275题
1.等差数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.在△ABC中,tanA是以

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知等差数列{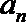
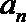
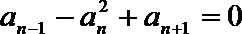
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.将正偶数排列如下表,其中第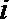
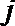
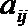
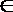
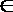
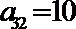
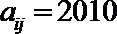
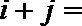
正确答案
60
解析
解析已在路上飞奔,马上就到!
知识点
20.已知


(1)若

(2)求证:对任意

正确答案
(1)依题意





所以
解得
(2)
设
则
考虑到
所以
又当

从而

所以对任意

解析
解析已在路上飞奔,马上就到!
知识点
4.设

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.设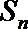
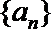
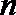
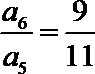
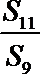
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16. 设等差数列{an}的前n项和为Sn,且S4=4S2,a2n=2an+1.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)证明:对一切正整数n,有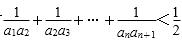
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.在



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.已知△ABC的三边长为a、b、c,若
正确答案
(用反证法证明1)
∵


∴
∴b2≤ac 即ac-b2≥0.
假设B是钝角,则cosB<0,
由余弦定理可得,

这与cosB<0矛盾,故假设不成立.
∴B不可能是钝角.
(用反证法证明2)
∵


∴
假设B是钝角,则
则B是△ABC的最大内角,所以b>a,b>c,
(在三角形中,大角对大边),
从而

故假设不成立,因此B不可能是钝角.
(用综合法证明)
∵


∴
证明:∵


∴
由余弦定理和基本不等式可得,

∵a,b,c为△ABC三边,∴a+c>b,
∴
∴cosB>0,
∴∠B<900,因此B不可能是钝角.
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析