- 等差数列的性质及应用
- 共275题
1
题型:简答题
|
20.已知


(1)若

(2)求证:对任意

正确答案
(1)依题意





所以
解得
(2)
设
则
考虑到
所以
又当

从而

所以对任意

解析
解析已在路上飞奔,马上就到!
知识点
等差数列的性质及应用不等式恒成立问题二项式系数的和或各项系数的和问题二项式定理的应用
1
题型:
单选题
|
4.设

正确答案
C
解析
解析已在路上飞奔,马上就到!
知识点
等差数列的基本运算等差数列的性质及应用等差数列的前n项和及其最值
1
题型:
单选题
|
5.设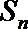
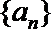
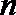
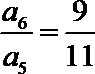
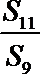
正确答案
A
解析
解析已在路上飞奔,马上就到!
知识点
等差数列的基本运算等差数列的性质及应用等差数列的前n项和及其最值
1
题型:简答题
|
16. 设等差数列{an}的前n项和为Sn,且S4=4S2,a2n=2an+1.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)证明:对一切正整数n,有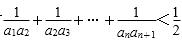
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
由递推关系式求数列的通项公式等差数列的基本运算等差数列的性质及应用裂项相消法求和数列与不等式的综合
1
题型:简答题
|
18.已知△ABC的三边长为a、b、c,若
正确答案
(用反证法证明1)
∵


∴
∴b2≤ac 即ac-b2≥0.
假设B是钝角,则cosB<0,
由余弦定理可得,

这与cosB<0矛盾,故假设不成立.
∴B不可能是钝角.
(用反证法证明2)
∵


∴
假设B是钝角,则
则B是△ABC的最大内角,所以b>a,b>c,
(在三角形中,大角对大边),
从而

故假设不成立,因此B不可能是钝角.
(用综合法证明)
∵


∴
证明:∵


∴
由余弦定理和基本不等式可得,

∵a,b,c为△ABC三边,∴a+c>b,
∴
∴cosB>0,
∴∠B<900,因此B不可能是钝角.
解析
解析已在路上飞奔,马上就到!
知识点
等差数列的性质及应用反证法的应用
下一知识点 : 等差数列的前n项和及其最值
扫码查看完整答案与解析










