- 等差数列的性质及应用
- 共275题
8.已知等差数列{an}的前n项和为Sn,若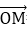
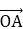
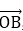
正确答案
2015
解析
若O,A,B,M为平面内四点,则A,B,M三点在一条直线上,当且仅当存在一对实数m,n,使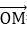
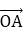

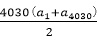
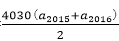
知识点
9.设F是椭圆

正确答案
解析
若公差d>0,则|FP1|最小,

并设为第n项,
则
注意到d>0,得
若d<0,易得
那么d的取值范围为
知识点
4.对大于1的自然数m的三次幂可用奇数进行以下方式的“分裂”,23


正确答案
解析
由题意知,自然数m的三次幂可用m个连续奇数进行“分裂”,把1算在内,从13到m3用从1开始的连续奇数共有1+2+3+…+m=


知识点
6.已知圆P:x2+y2=4y及抛物线S:x2=8y,过圆心P作直线 l,此直线与上述两条曲线的四个交点,自左向右顺次记为A,B,C,D,如果|AB|,|BC|,|CD|按此顺序构成一个等差数列,则直线l的斜率为( ).
正确答案
解析
由题意可知,圆P的圆心坐标为(0,2),半径为2,抛物线S的焦点为(0,2),准线方程为y=-2,画出图象如图所示,其中|BC|=4.由于|AB|,|BC|,|CD|成等差数列,所以|AB|+|CD|=8,所以|AB|+|BC|+|CD|=12,则所求问题等价于当过抛物线S的焦点的直线被抛物线所截得的线段的长度为12时,求直线的斜率.设A(x1,y1),D(x2,y2),过A,D分别向抛物线的准线作垂线,垂足分别为A',D'.根据抛物线定义得|AP|=|AA'|=y1+2,|DP|=|DD'|=y2+2,所以|AD|=|AP|+|DP|=y1+y2+4=12,得y1+y2=8.由题意可知,直线l的斜率存在,且不为0.设直线l的斜率为k(k≠0),则直线l的方程为y=kx+2,即x=

知识点
17.等比数列

(Ⅰ)求数列
(Ⅱ)设


正确答案
解:
(Ⅰ)设数列{an}的公比为q,由


由条件可知

由


(Ⅱ )
故
所以数列
解析
解析已在路上飞奔,马上就到!
知识点
1.若1,a,3成等差数列;1,b,4成等比数列,则
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.如图,将所有正奇数排成一个三角形数据库:根据排列规律,第n(n≥2)行从左向右数的第2个数为________.
正确答案
n2-n+3
解析
把各行的第2个数表示如下,a2=5,a3=9,a4=15,a5=23,…,则a3-a2=4=2×2,a4-a3=6=2×3,a5-a4=8=2×4,…,an-an-1=2×(n-1),将以上式子相加可得an=a2+
知识点
14.已知数列 的前n项和Sn=10n-n2(n∈N+),则数列 的前n项和Tn为 .
正确答案
解析
当n=1时,a1=S1=9;当n≥2时,an=Sn-Sn-1=11-2n,
由于n=1时,a1=9也满足11-2n,
因此an=11-2n.
(1)当n>5时,
(2)当n≤5时,
综合(1)(2),得
知识点
7.已知a > 0,b > 0,a、b的等差中项是

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知数列是公比为q的等比数列,且a2,a4,a3成等差数列,则q=______
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析