- 等差数列的性质及应用
- 共275题
已知数列


(1)证明数列
(2)求通项

(3)设


正确答案
见解析
解析
(1)因为


又


所以


(2)由


所以
由错项相减得
(3)因为
由于
所以,

因为集合

所以
知识点
已知数列





正确答案
解析
由等差数列








知识点
已知数列



(1)求数列
(2)求证:

正确答案
见解析。
解析
(1)由

所以




(2)(方法一)


因为

(方法二)


因为

知识点
在等差数列{an}中,a3+a4+a5=84,a9=73.
(1)求数列{an}的通项公式;
(2)对任意m∈N﹡,将数列{an}中落入区间(9m,92m)内的项的个数记为bm,求数列{bm}的前m项和Sm。
正确答案
(1)
(2)
解析
(1)由a3+a4+a5=84,a5=73可得




(2)对任意m∈N﹡,

即


于是

即
知识点
设等比数列




(1)求数列
(2)在




求证:

正确答案
见解析。
解析
(1)设等比数列






即

当


即
(2)①

设

① -②得:
=
知识点
公差不为零的等差数列




正确答案
8192
解析
等差数列


取

知识点
等差数列


正确答案
解析
略。
知识点
设













正确答案
2或4
解析




由题可知,点









由




令
由等式



故当


当

知识点
若数列{an}的前n项和为Sn,则下列命题正确的是( )
正确答案
解析
解:A:数列{an}的前n项和为Sn,故 Sn =a1+a2+a3+…+an,
若数列{an}是递增数列,则数列{Sn}不一定是递增数列,如an=n﹣60,当an<0 时,数列{Sn}是递减数列,故A不正确。
B:由数列{Sn}是递增数列,不能推出数列{an}的各项均为正数,
如数列:0,1,2,3,…,满足{Sn}是递增数列,但不满足数列{an}的各项均为正数,故B不正确。
C:若{an}是等差数列(公差d≠0),则由S1•S2…Sk=0不能推出a1•a2…ak=0,
例如数列:﹣3,﹣1,1,3,满足S4=0,但 a1•a2•a3•a4≠0,故C不正确。
D:一方面:若{an}是等比数列,则由S1•S2…Sk=0(k≥2,k∈N),
从而当k=2时,有S1•S2=0⇒S2=0⇒a1+a2=0,
∴a2=﹣a1,从而数列的{an}公比为﹣1,故有ak+ak+1=ak﹣ak=0。
另一方面,由ak+ak+1=0可得ak=﹣ak+1,∴a2=﹣a1,
可得S2=0,∴S1•S2…Sk=0(k≥2,k∈N),故D正确。
故选D。
知识点
等差数列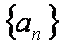
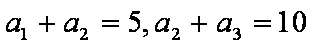
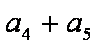
正确答案
20
解析
设数列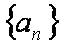
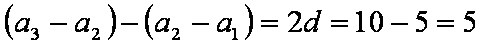

知识点
扫码查看完整答案与解析













































