等差数列的性质及应用
共275题

· 等差数列的性质及应用

等差数列的性质及应用
共275题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

在等差数列，则此数列前10项的和

A45

B60

C75

D90

正确答案

解析

略

知识点

等差数列的性质及应用等差数列的前n项和及其最值

题型：单选题

单选题 · 5 分

已知等差数列中,,前7项和,则等于

A18

B20

C24

D32

正确答案

解析

略

知识点

等差数列的基本运算等差数列的性质及应用等差数列的前n项和及其最值

题型：简答题

简答题 · 13 分

已知集合，

具有性质：对任意的，至少有一个属于。

（1）分别判断集合与是否具有性质；

（2）求证：①；

②；

（3）当或时集合中的数列是否一定成等差数列?说明理由。

正确答案

见解析

解析

（1）集合具有性质，

，，集合不具有性质，———3分

（2）由已知，，

则，仍由知；———5分

，，

———6分

将上述各式两边相加得

，即；———8分

（3）当时，集合中的数列一定是等差数列。

由（2）知，且，

故，而这里，反之若不然

这与集合中元素互异矛盾，只能，即

成等差数列， ———9分

当时，集合中的元素不一定是等差数列。

如，中元素成等差数列，

又如，中元素不成等差数列；———11分

当5时，集合中的元素一定成等差数列

证明：

令①②

②①有，且由①

，

又，

成等差数列， ———13分

知识点

等差数列的性质及应用

题型：简答题

简答题 · 12 分

已知等差数列 ;等比数列，

。

（1）求数列和数列的通项公式；

（2）设，求数列的前n项和。

正确答案

见解析。

解析

知识点

等差数列的性质及应用

题型：填空题

填空题 · 4 分

已知数列是公差为2的等差数列，是的前n项和，则= 。

正确答案

解析

略

知识点

等差数列的性质及应用

题型：简答题

简答题 · 12 分

已知定点,,动点,且满足成等差数列。

（1）求点的轨迹的方程；

（2）若曲线的方程为(),过点的直线与曲线相切,求直线被曲线截得的线段长的最小值。

正确答案

见解析。

解析

（1）由,,

根据椭圆定义知的轨迹为以为焦点的椭圆,

其长轴,焦距,短半轴,故的方程为.

（2）过点与X轴垂直的直线不与圆相切，故可设:,由直线与曲线

相切得,化简得

由,解得

联立,消去整理得,

直线被曲线截得的线段一端点为,设另一端点为,解方程可得,有

令,则,

考查函数的性质知在区间上是增函数,

所以时,取最大值,从而.

知识点

等差数列的性质及应用直接法求轨迹方程直线、圆及圆锥曲线的交汇问题

题型：填空题

填空题 · 4 分

已知首项的无穷等比数列的各项和等于4，则这个数列的公比是。

正确答案

解析

略

知识点

等差数列的性质及应用

题型：填空题

填空题 · 4 分

若等差数列的首项为公差为，前项的和为，则数列为等差数列，且通项为，类似地，请完成下列命题：若各项均为正数的等比数列的首项为，公比为，前项的积为，则。

正确答案

数列为等比数列，且通项为

解析

略

知识点

等差数列的性质及应用

题型：简答题

简答题 · 18 分

若正项数列满足条件：存在正整数，使得对一切都成立，则称数列为级等比数列。

（1）已知数列为2级等比数列，且前四项分别为，求的值；

（2）若为常数），且是级等比数列，求所有可能值的集合，并求取最小正值时数列的前项和；

（3）证明：为等比数列的充要条件是既为级等比数列，也为级等比数列。

正确答案

见解析

解析

（1）

（2）是级等比数列，

所以，

最小正值等于，此时

，，

（3）充分性：若为等比数列，则

对一切成立，显然对成立。

所以既为级等比数列，也为级等比数列。

必要性：若为级等比数列，，则均成等比数列，设等比数列的公比分别为，为级等比数列，，则成等比数列，设公比为

既是中的项，也是中的项，

设，则

所以（），（），

又，，

所以，

（）

所以，，（）

综合得：，显然为等比数列。

知识点

等差数列的性质及应用

题型：简答题

简答题 · 12 分

已知椭圆过点（0，1），其长轴、焦距和短轴的长的平方依次成等差数列.直线轴正半轴和y轴分别交于Q、P，与椭圆分别交于点M、N，各点均不重合且满足.

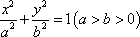
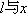
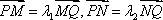
（1）求椭圆的标准方程；

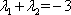
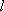
（2）若，试证明：直线过定点并求此定点.

正确答案

见解析

解析

知识点

向量在几何中的应用等差数列的性质及应用椭圆的定义及标准方程直线、圆及圆锥曲线的交汇问题

继续学习学习下一知识点

下一知识点 : 等差数列的前n项和及其最值

百度题库 > 高考 > 理科数学 > 等差数列的性质及应用

扫码查看完整答案与解析