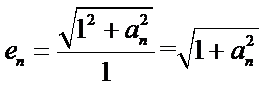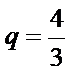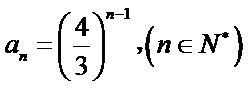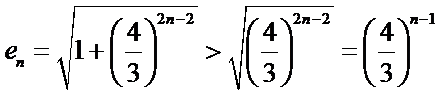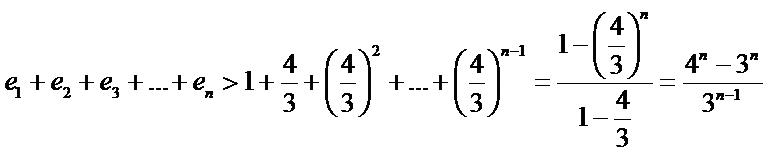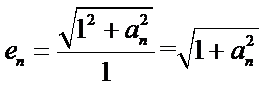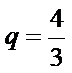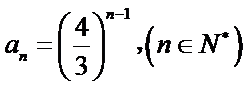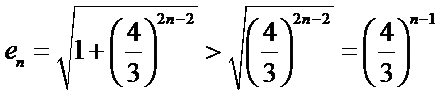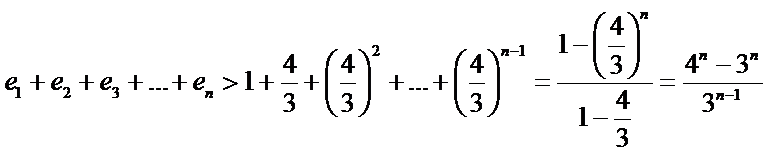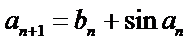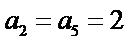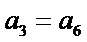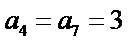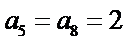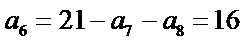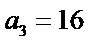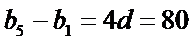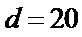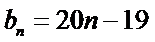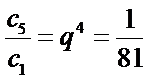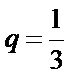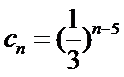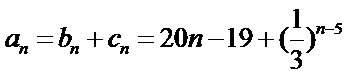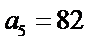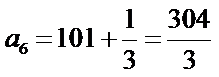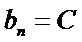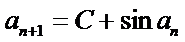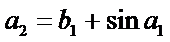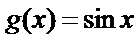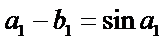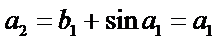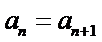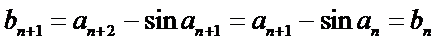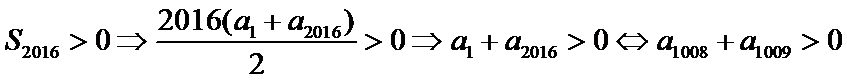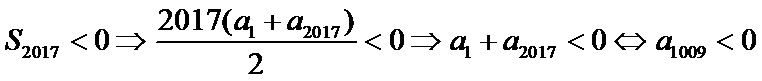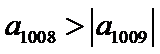- 等差数列的性质及应用
- 共275题
已知数列{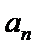
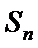
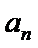
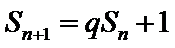
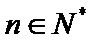
23.若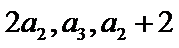
24.设双曲线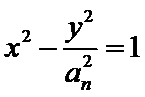
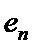
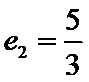
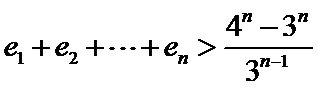
正确答案
(Ⅰ)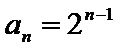
解析
(Ⅰ)由已知,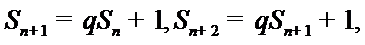
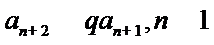
又由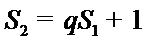
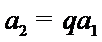
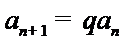
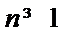
所以,数列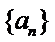
从而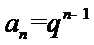
由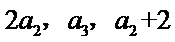
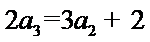
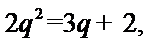
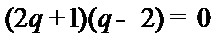
由已知,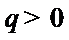
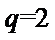
所以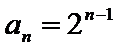
考查方向
解题思路
本题考查数列的通项公式、双曲线的离心率、等比数列的求和公式等基础知识,考查学生的分析问题解决问题的能力、计算能力.在第(Ⅰ)问中,已知的是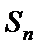
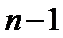
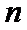
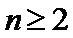
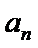
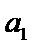
易错点
本题考查数列的通项公式、双曲线的离心率、等比数列的求和公式等基础知识,考查学生的分析问题解决问题的能力、计算能力.在第二问易错
正确答案
(II)证明:由双曲线的性质可知,
由(I)可得,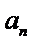
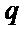
故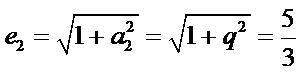
∴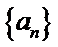
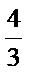
∴
∴
原式得证.
解析
(II)证明:由双曲线的性质可知,
由(I)可得,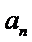
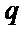
故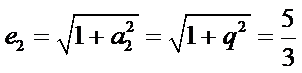
∴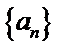
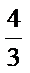
∴
∴
原式得证.
考查方向
解题思路
本题考查数列的通项公式、双曲线的离心率、等比数列的求和公式等基础知识,考查学生的分析问题解决问题的能力、计算能力.在第(Ⅱ)问中,不等式的证明用到了放缩法,这是证明不等式常用的方法,本题放缩的目的是为了求数列的和.另外放缩时要注意放缩的“度”.不能太大,否
易错点
本题考查数列的通项公式、双曲线的离心率、等比数列的求和公式等基础知识,考查学生的分析问题解决问题的能力、计算能力.在第二问易错
若无穷数列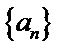

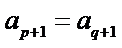

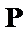
28.若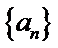
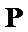
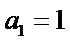
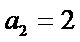
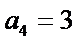
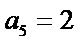
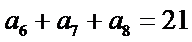
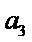
29.若无穷数列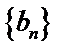
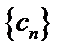
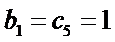
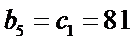
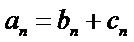
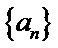
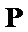
30.设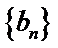
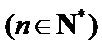
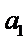
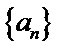
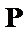
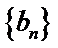
正确答案
解析
由题意知
∴
∴
∴
∴
∴
考查方向
解题思路
反复利用性质求解
易错点
对新定义的性质的不理解;
正确答案
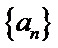
解析
设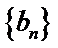
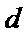
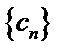
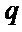
∴
∴
∴
∴
∴
∵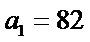
而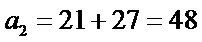
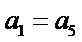
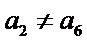
故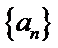
考查方向
解题思路
通过计算,寻找不符合性质的情形“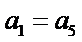
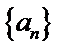
易错点
寻找不到反例
正确答案

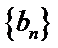
解析
充分性:若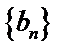
则
若存在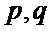
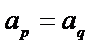
则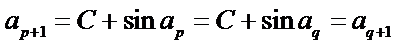
故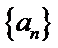
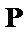
必要性:若对任意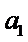
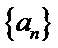
则
设函数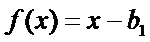
由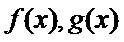
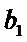
∴一定能找到一个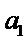
∴
∴
故
∴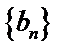
考查方向
解题思路
从充分性和必要性两方面入手证明.
易错点
充要条件的证明.
已知数列



24. 若


25.设





26. 设







正确答案
(1)
解析
试题分析: (1)把bn=3n+5代入已知递推式可得an+1-an=6,由此得到{an}是等差数列,则an可求.
(1)解:由

所以


故


考查方向
解题思路
等差数列的四种判断方法:(1)定义法:an+1-an=d(d是常数)⇔{an}是等差数列;(2)等差中项法:2an+1=an+an+2(n∈N*)⇔{an}是等差数列;(3)通项公式:an=pn+q(p,q为常数)⇔{an}是等差数列;(4)前n项和公式:Sn=An2+Bn(A、B为常数)⇔{an}是等差数列.
易错点
等差数列性质的灵活运用
正确答案
(2)略.
解析
试题分析:(2)由


证明:(2)由

所以


因为



故

考查方向
解题思路
数列作为特殊的函数,其单调性的判断与研究也是特别的,只需研究相邻两项之间关系即可.
易错点
数列的单调性
正确答案
(3)
解析
试题分析:(3)由(2)可得

(3)因为

当

当

所以
因为


①当

②当




③当






综上,

考查方向
解题思路
数列作为特殊的函数,其单调性的判断与研究也是特别的,只需研究相邻两项之间关系即可.
易错点
分类讨论的不重不漏
6.已知等差数列



正确答案
2
解析
设







考查方向
解题思路
本题考查运用等差数列及等比数列性质求首项,解题步骤如下:设







易错点
本题必须注意审题,忽视则会出现错误。
知识点
9.设等差数列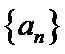
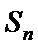
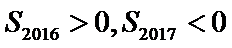
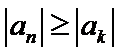
正确答案
解析
∵
故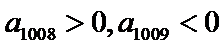
∴对任意正整数n,都有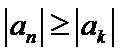
考查方向
解题思路
由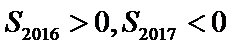
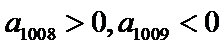
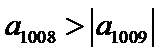
易错点
本题不易在利用前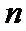
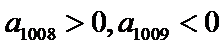
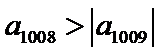
知识点
19. 设等差数列
(I)求数列
(II)记

正确答案
(1)
(2)
解析
试题分析:本题属于数列应用中的基本问题,题目的难度是逐渐由易到难
(Ⅰ)设等差数列的




由题意可知:
所以

(Ⅱ)令
相减得

考查方向
解题思路
本题考查数列的性质,解题步骤如下:
1、利用基本量法求出通项;
2、利用错位相减法求和
易错点
第一问中的易计算出现问题。
知识点
14. 已知数列



正确答案
解析
因为






考查方向
解题思路
根据通项和前n项和的关系和已知条件求解。
易错点
找不到通项和前n项和的关系
知识点
3.已知等差数列





正确答案
解析
考查方向
解题思路
利用等差数列的通项公式及其前n项和公式即可得出.
易错点
第8 项和第9项最大问题。
知识点
设等差数列





20.求数列

21.当



正确答案
(Ⅰ)

解析
(Ⅰ)由题意有,


故

考查方向
解题思路
(Ⅰ)由已知可列出方程组
易错点
公式记错。
正确答案
(Ⅱ)
解析
由





①-②可得

故
考查方向
解题思路
(Ⅱ)由(Ⅰ)可得



易错点
不知道用错位相减法求和。
已知数列{an}满足:a1=c,2an+1=an+l(c≠1,n∈N*),记数列{an}的前n项和为Sn.
18.令bn=an一l,证明:数列{bn}是等比数列;
19.求最小的实数c,使得对任意n∈N*,都有Sn≥3成立.
正确答案
见解析
解析
解题思路
易错点
数列{bn}的首项问题,求最小值时候的讨论。
正确答案
解析
解题思路
易错点
数列{bn}的首项问题,求最小值时候的讨论。
扫码查看完整答案与解析