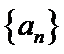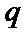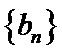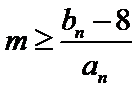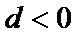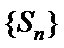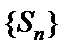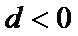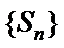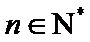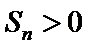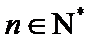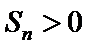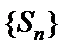- 等差数列的性质及应用
- 共275题
18. 已知等比数列
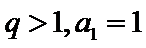
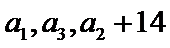
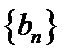
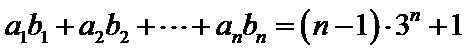
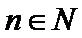
(I)求数列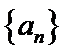
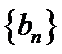
(II)若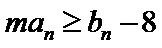
正确答案
见解析
解析
考查方向
解题思路
1)借助等差数列性质求出
2)利用由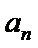
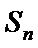
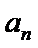
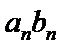
3)对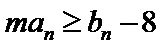
4)讨论新数列单调性,并求出最值
易错点
本题第一问忽略验证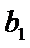
知识点
12.在公差不为







正确答案
解析
在等差数列中由








因此A选项不正确,B选项不正确,D选项不正确,所以选C选项。
考查方向
解题思路
1.在等差数列中由






易错点
求
知识点
已知等比数列



22.求数列

23.求数列

正确答案
(1)
解析
(1)设

故方程有两个不同的实根,由
从而

考查方向
解题思路
1)第一问设




2)第二问
易错点
错位相减法求和计算容易错。
正确答案
(2)
解析
(2)由(1)知
考查方向
解题思路
1)第一问设




2)第二问
易错点
错位相减法求和计算容易错。
5.等差数列








正确答案
解析
考查方向
解题思路
1、使用一元二次不等式解集求参数的值d,a1,
2、使用通项公式确定前n项和的最大值
易错点
主要易错于最值的判断
知识点
2.在等差数列



正确答案
解析
由等差数列的性质得
考查方向
解题思路
本题可以直接利用等差数列的通项公式求解,也可应用等差数列的性质求解,主要考查学生灵活应用基础知识的能力.
易错点
等差数列性质
知识点
6. 设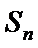
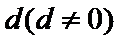
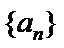
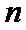
正确答案
解析
通过对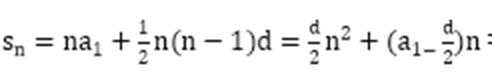
考查方向
解题思路
根据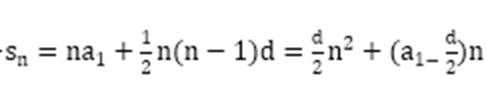
易错点
对等差数列的前n项和公式的函数性质没有掌握
知识点
7.在等比数列




正确答案
解析
在等比数列








考查方向
解题思路
在等比数列






易错点
由
知识点
5.已知Sn为等差数列{an}的前n项和,若S3+S7= 37,则
正确答案
解析
由




故A选项不正确,B选项不正确,C选项不正确,所以选D选项。
考查方向
解题思路
根据等差数列的性质求出
故A选项不正确,B选项不正确,C选项不正确,所以选D选项。
易错点
找不到已知和所求间的内在联系出错。
知识点
3.在等差数列


正确答案
解析
因为



考查方向
解题思路
1.先将


易错点
本题容易在用等差数列性质时出现错误.
知识点
已知






22.求数列

23.设






正确答案
(1)
解析
(1)因为

所以



所以
考查方向
解题思路
1.第(1)问根据等差数列、等比数列的基本量求出通项公式;2.根据第(1)问求出
易错点
1.不会将


正确答案
(1)
解析
(2)

所以

(或
因为



所以,不存在正整数

考查方向
解题思路
1.第(1)问根据等差数列、等比数列的基本量求出通项公式;2.根据第(1)问求出
易错点
1.不会将


扫码查看完整答案与解析