- 等差数列的性质及应用
- 共275题
对于数列



对于正整数









正确答案
26
解析
略
知识点
设数列
正确答案
解析
略
知识点
等差数列









正确答案

解析
略
知识点
已知数列



(1)若



(2)证明:数列




正确答案
见解析
解析
(1)因为对任意

所以
所以
即
所以数列
所以
(2)(1)充分性:若对于任意



所以
即
因为当


所以
因为
所以
即数列


(2)必要性:若数列



因为
所以



即




………13分
综上所述,数列



知识点
已知数列
(1)
(2)数列
正确答案
见解析。
解析
知识点
已知等差数列



(1)求数列

(2)设数列




正确答案
(1)
(2)
解析
(1)由题意




又

(2) 
又
①

当
当
所以,
知识点
设Sn表示数列
(1) 若
(2)若


正确答案
见解析。
解析
解:(1)
(注:只要写对其中一个公式便算对,直接写
的扣1分)
证明:因为
所以
将①式乘以公比

①-②得:
所以当
当
因此
(注:由于证明等比数列前

(2)证明:因为
所以
所以
因此
则
知识点
已知数列





正确答案
解析
由等差数列








知识点
设等差数列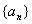
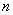
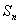
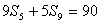
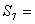
正确答案
7
解析
略
知识点
已知数列




(1)求
(2)设

正确答案
见解析。
解析
(1)设等差数列的公差为

因为

从而


所以
(2)依题意

由于
综上所述
知识点
扫码查看完整答案与解析
















































