- 等差数列的性质及应用
- 共275题
对于数列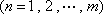

















定义数列






(1)当






(2)是否存在数列

正确答案
见解析。
解析
(1)由题意,创新数列为










数列




(2)存在数列



因为

所以
由题意知,



所以

若

则

当








此时数列


当







此时数列





当

又






综上,当数列







知识点
在如图所示的数表中,第










正确答案
16;
解析
略
知识点
设等差数列





(1)求A;
(2)求数列
(3)若
正确答案
见解析。
解析
(1)由

(2)令
当n=1时,a1=S1=2,当n≥2时,an=Sn-Sn-1=n2+n
综合之:an=2n
由题意
∴数列{cn+1}是

(3)当
当
综合之:
知识点
如果等差数列{an}中,a3+a4+a5=12,那么a1+a2+…+a7=( )
正确答案
解析
a3+a4+a5=3a4=12,a4=4,
知识点
等差数列

正确答案
14
解析
略
知识点
扫码查看完整答案与解析























