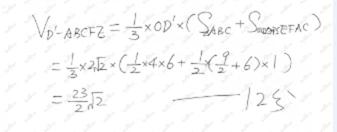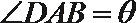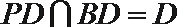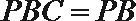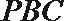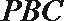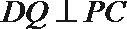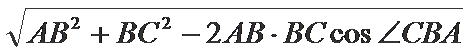- 直线、平面垂直的判定与性质
- 共445题
10.如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的表面积为()
正确答案
知识点
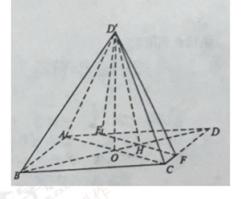
19. 如图,菱形ABCD的对角线AC与BD交于点O,点E,F分别在AD,CD上,AE=CF,EF交BD于点H,将△DEF沿EF折到△D′EF的位置.
(I)证明: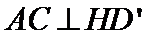
(II)若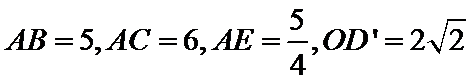
正确答案
知识点
18. 在如图所示的几何体中,D是AC的中点,EF∥DB.
(I)已知AB=BC,AE=EC.求证:AC⊥FB;
(II)已知G,H分别是EC和FB的中点.求证:GH∥平面ABC.
正确答案
(Ⅰ))证明:见解析;(Ⅱ)见解析.
解析
试题分析:(Ⅰ))根据








(Ⅱ)设








试题解析:(Ⅰ))证明:因













(Ⅱ)设



















考查方向
知识点
19. 如图,菱形ABCD的对角线AC与BD交于点O,点E,F分别在AD,CD上,AE=CF,EF交BD于点H,将△DEF沿EF折到△D′EF的位置.
(I)证明:
(II)若
正确答案
(I)由已知得,
又由

由此得

(II)由
由
所以
于是
由(I)知

所以

又由

又由
五边形
所以五棱锥
知识点
19.如图,在直三棱柱




(Ⅰ)求证:

(Ⅱ)试在棱


正确答案
(Ⅰ)(略)
(Ⅱ)当

解析
试题分析:本题属于立体几何中线面关系的位置关系的问题,难度不大,只要熟悉了线面关系中平行与垂直的判定和性质定理,即可完成。
(Ⅰ)连结



在


又因为


因为



所以

(Ⅱ)当


因为在直三棱柱

所以四边形
因为




所以
又因为
所以

因为


所以
因为平面




所以
因为


因为


所以

因为


考查方向
解题思路
本题主要考查直线与直线、直线与平面及平面与平面的位置关系,
解题步骤如下:由线线平行推出线面平行;由面面垂直推出线面垂直,从而得出线线垂直。
易错点
第一问在书写时易遗漏



第二问在线面垂直的转化中易混淆不清。
知识点
19.(本小题满分12分)如图,已知四棱锥


(Ⅰ)证明:
(Ⅱ)若

正确答案
见解析
解析
(Ⅰ)
证明:取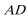





又






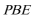

(Ⅱ)
由(Ⅰ)






由侧面





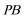
考查方向
解题思路
作出适当的辅助线,根据线面垂直证明线线垂直
易错点
找垂直条件时找不到
知识点
19.如图所示,三棱锥







(Ⅰ)若过点






(Ⅱ)求点

正确答案
(Ⅰ)

(Ⅱ)
解析
(Ⅰ)当





(Ⅱ)因为

所以直线



又
所以
设点



所以

又

设点



即




考查方向
解题思路
第一问,过O点做AC和CD的平行线即可;第二问用体积相等
易错点
第二问求出
知识点
19. 四棱锥
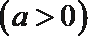
(1)若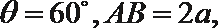
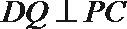
(2)若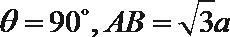
正确答案
详细答案见解析.
解析
试题分析:本题属于三角函数的图像与性质及正余弦定理的综合应用问题,属于简单题,只要掌握相关函数的知识,即可解决本题,解析如下:
证明(1)连结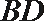
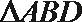
由余弦理: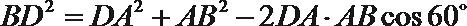
解得
所以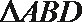
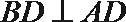
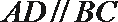
所以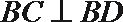
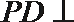
所以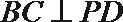
所以
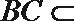
所以,平面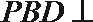
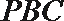
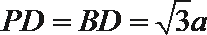
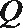
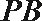
所以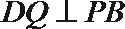
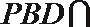
所以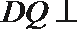
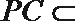
所以
(2) 当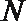
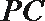
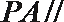
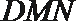
证明:连结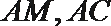
设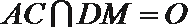
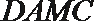
由中点得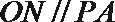
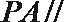
考查方向
本题考查了线面平行、垂直,余弦定理的相关知识点。
易错点
证明线面垂直时由于不熟悉定理容易证错。
知识点
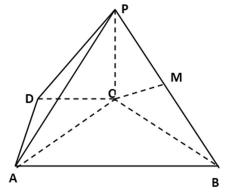
16.在四棱锥P-ABCD中,PC⊥平面ABCD,DC∥AB,DC=2,AB=4,BC=2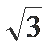
(1)求证:AC⊥PB;
(2)若PC=2,点M是棱PB上的点,且CM∥平面PAD,求BM的长。
正确答案
见解析
解析
(1)∵PC⊥平面ABCD,∴PC⊥AC,
又∠CBA=30°,BC=2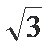
∴AC=
=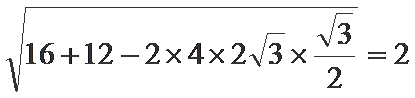
∴AC2+BC2=4+12=16=AB2,∴∠ACB=90°,
故AC⊥BC.又∵PC、BC是平面PBC内的两条相交直线,
故AC⊥平面PBC,∴AC⊥PB.
(2) BM=2
考查方向
解题思路
(1)由余弦定理求AC
(2)由勾股逆定理得∠ACB=90°
(3)AC⊥BC,PC⊥AC,AC⊥平面PBC,∴AC⊥PB
易错点
证明过程不到位。
知识点
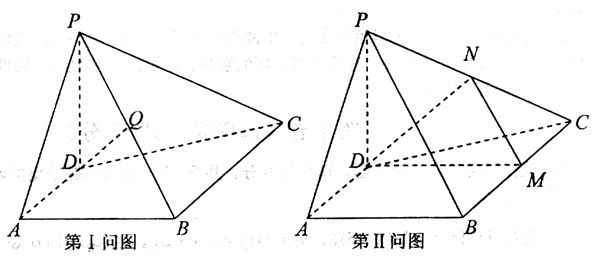
19.如图,在三棱锥









(1)求证:

(2)当

正确答案
(2)
解析
(1)证明:






又






又已知


(2)



而


又

又


而




考查方向
本题主要考查了棱柱、棱锥、棱台的体积;平面与平面垂直的判定.
解题思路
(1)利用面面垂直的判定定理证明平面SAC⊥平面AMN.
(2)利用VS-ACM=VD-ACM=VM-DAC,即可求三棱锥S-ACM的体积.
易错点
(1)利用线面垂直条件证明,注意要垂直两条相交直线
(2)利用等体积法求
知识点
扫码查看完整答案与解析