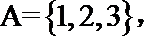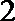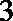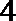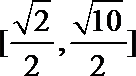空间图形的公理
共69题

· 空间图形的公理

空间图形的公理
共69题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 15 分

如图，在三棱台中，已知平面BCFE平面ABC，，，，，

（Ⅰ）求证：

（Ⅱ）求二面角的余弦值.

正确答案

（I）延长，，相交于一点，如图所示．

因为平面平面，且，所以，

平面，因此，

．

又因为，，，所以

为等边三角形，且为的中点，则

．

所以平面．

过点作，连结．

因为平面，以，则平面，所以．

所以，是二面角的平面角．

在中，，，得．

所以，二面角的平面角的余弦值为．

知识点

空间图形的公理

题型：简答题

简答题 · 13 分

17.如图，正方形ABCD的中心为O，四边形OBEF为矩形，平面OBEF⊥平面ABCD，点G为AB的中点，AB=BE=2.

（I）求证：EG∥平面ADF；

（II）求二面角O-EF-C的正弦值；

（III）设H为线段AF上的点，且AH=HF，求直线BH和平面CEF所成角的正弦值.

正确答案

知识点

空间图形的公理

题型：填空题

填空题 · 5 分

13.如图，在△ABC中，D是BC的中点，E，F是AD上的两个三等分点，·=4，，则的值是 .

正确答案

知识点

空间图形的公理

题型：简答题

简答题 · 12 分

如图，在四棱锥中，底面ABCD为边长为的正方形，

21.求证：

22．若E,F分别为PC,AB的中点，平面求三棱锥的体积.

第(1)小题正确答案及相关解析

正确答案

见解析

解析

连接交于点，因为底面是正方形，所以且为的中点. 又所以平面，由于平面,故.又,故.

考查方向

空间几何体,直线与平面的角

解题思路

第一问根据正方形的相关性质进行证明,第二问先求出底面的面积，然后找到三棱锥的高，利用三棱锥的体积公式求解。

易错点

立体感不强，计算能力弱

第(2)小题正确答案及相关解析

正确答案

见解析

解析

设的中点为,连接,∥=,所以为平行四边形，∥，因为平面，所以平面，所以,的中点为,所以.由平面，又可得，又，又，所以平面，所以,又，所以平面。

（注意：没有证明出平面，直接运用这一结论的，后续过程不给分）

，故三棱锥D-ACE的体积为.

考查方向

空间几何体,直线与平面的角

解题思路

第一问根据正方形的相关性质进行证明,第二问先求出底面的面积，然后找到三棱锥的高，利用三棱锥的体积公式求解。

易错点

立体感不强，计算能力弱

题型：单选题

单选题 · 5 分

1．已知集合则B中所含元素的个数为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

空间图形的公理

题型：填空题

填空题 · 5 分

14. 若，且，，，则大小关系为____________。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

空间图形的公理

题型：单选题

单选题 · 5 分

9．设集合，，若动点，则的取值范围是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

空间图形的公理

题型：单选题

单选题 · 5 分

3.若函数在[1,+∞)上的最大值为,则实数a的值为（　　　　）

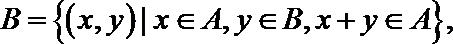
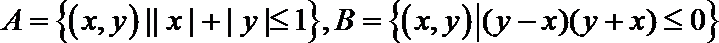
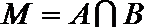
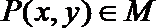
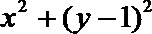
正确答案

解析

若a>1,当x>时,

f'(x)<0,f(x)单调递减,

当时,

f'(x)>0,f(x)单调递增,

当时,

令不合题意

若0<a≤1,则f'(x)≤0,f(x)在[1,+∞)上单调递减,

故‍，

解得.

知识点

空间图形的公理

题型：单选题

单选题 · 5 分

12．已知数列满足，，则（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

空间图形的公理

棒棒哒，已学完当前知识点学习下一知识点

下一知识点 : 异面直线及其所成的角

百度题库 > 高考 > 理科数学 > 空间图形的公理

扫码查看完整答案与解析