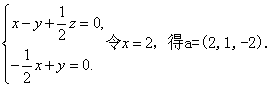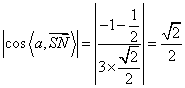- 异面直线及其所成的角
- 共103题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
如图,在四面体







(1)若



(2)若二面角





正确答案
见解析
解析
(1)如图所示,设F为AC的中点,由于AD=CD,所以DF⊥AC.
故由平面







故四面体ABCD的体积
(2)如图所示设G、H分别为变CD,BD的中点,则FG//AD,GH//BC,,从而


设E为边AB的中点,则EF//BC,由











在

从而
因





故异面直线

知识点
直三棱柱ABCA1B1C1中,∠BCA=90°,M,N分别是A1B1,A1C1的中点,BC=CA=CC1,则BM与AN所成角的余弦值为( )
正确答案
解析
知识点
若圆心在





正确答案

解析
设圆心为


知识点
过正方体



正确答案
解析
考查空间感和线线夹角的计算和判断,重点考查学生分类、划归转化的能力。第一类:通过点A位于三条棱之间的直线有一条体对角线AC1,第二类:在图形外部和每条棱的外角和另2条棱夹角相等,有3条,合计4条。
知识点
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=900。
(1)求证:PC⊥BC;
(2)求点A到平面PBC的距离。
正确答案
见解析。
解析
(1)证明:因为PD⊥平面ABCD,BC
由∠BCD=900,得CD⊥BC,
又PD

所以BC⊥平面PCD。
因为PC
(2)
(方法一)分别取AB、PC的中点E、F,连DE、DF,则:
易证DE∥CB,DE∥平面PBC,点D、E到平面PBC的距离相等。
又点A到平面PBC的距离等于E到平面PBC的距离的2倍。
由(1)知:BC⊥平面PCD,所以平面PBC⊥平面PCD于PC,
因为PD=DC,PF=FC,所以DF⊥PC,所以DF⊥平面PBC于F。
易知DF=

(方法二)体积法:连结AC。设点A到平面PBC的距离为h。
因为AB∥DC,∠BCD=900,所以∠ABC=900。
从而AB=2,BC=1,得

由PD⊥平面ABCD及PD=1,得三棱锥P-ABC的体积
因为PD⊥平面ABCD,DC
又PD=DC=1,所以
由PC⊥BC,BC=1,得

由


故点A到平面PBC的距离等于
知识点
在长为12cm的线段AB上任取一点C.现作一矩形,领边长分别等于线段AC,CB的长,则该矩形面积小于32cm2的概率为
正确答案
解析
设线段AC的长为


由



知识点
一个长方体去掉一个小长方体,所得集合体的正(主)视图与侧(左)视图分别如下图所示,则该几何体的俯视图为
正确答案
解析
很容易看出这是一个面向我们的左上角缺了一小块长方体的图形,不难选出答案。
知识点
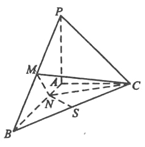
已知三棱锥P-ABC中,PA⊥ABC,AB⊥AC,PA=AC=½AB,N为AB上一点,AB=4AN,M,S分别为PB,BC的中点。
(1)证明:CM⊥SN;
(2)求SN与平面CMN所成角的大小。
正确答案
见解析。
解析
设PA=1,以A为原点,射线AB,AC,AP分别为x,y,z轴正向建立空间直角坐标系如图。
则P(0,0,1),C(0,1,0),B(2,0,0),M(1,0,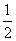
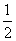
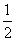
(1)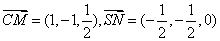
因为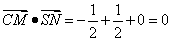
所以CM⊥SN
(2)
设a=(x,y,z)为平面CMN的一个法向量,
则
因为
所以SN与片面CMN所成角为45°。
知识点
扫码查看完整答案与解析