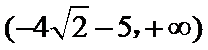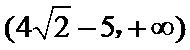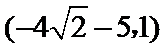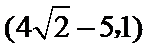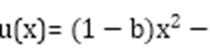- 函数的图象
- 共75题
20. 已知抛物线








(I)若




(II)若


正确答案
(Ⅰ)
由于


记




所以
;(Ⅱ)
解析
由题设



记过



(Ⅰ)由于


记




所以
(Ⅱ)设


则
由题设可得


设满足条件的

当



而

当




考查方向
解题思路
设出与X轴垂直的直线,得出点的坐标,通过证明直线斜率即可证明结果
易错点
注意应用坐标法证明时利用斜率关系,求轨迹时不可忽视分类讨论。
知识点
8.已知函数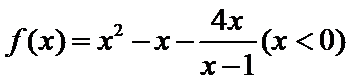
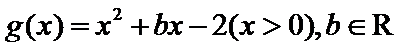
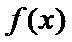
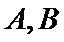
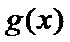
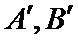
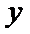
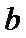
正确答案
解析
设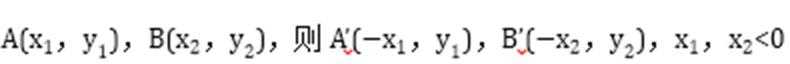

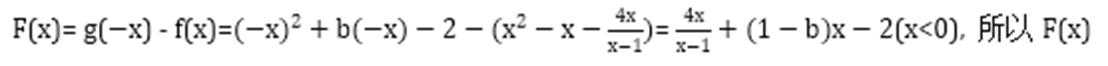
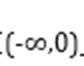
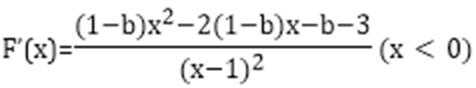
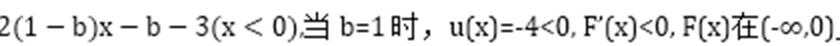
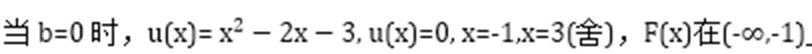
考查方向
解题思路
先设点,后转化方程,得到一个方程有两个负根的问题,然后再构造一个新函数,运用导数来判断函数的有关零点问题
易错点
不能正确理解题目中的对称问题,进而在问题转化过程中进行不下去,对不同情况进行分类讨论不全
知识点
12. 形如





正确答案
解析
令






所以 


所以 


在同一坐标系内的图象如图所示,图像交点个数为4 ,选C
考查方向
解题思路
1.先根据

2.根据“囧函数”的概念求出
3.在同一个坐标系下做出

易错点
1.不理解题中给出的“囧函数”的概念;
2.不会处理复合函数函数
知识点
14.若函数




正确答案
4,0,-16
解析
f(x-1)是偶函数,所以有f(x-1)= f(-x-1);所以有




考查方向
解题思路
根据题意,图像关于直线x=-1对称,所以将函数f(x)的图像向右平移一个单位,得到偶函数图像,再利用偶函数的性质,求出a与b,然后利用导数求函数的最小值
易错点
在对称性应用上易出错
知识点
10.如图所示,函数



正确答案
解析
设两个交点为A、B,由抛物线图象可知,令y=0,解得交点A(-









考查方向
解题思路
先根据两个图像的特殊性,求出两个交点的坐标,AB两点的水平距离恰为1/4周期,应用周期公式求出

易错点
不能正确的提炼图像中渗透的信息,没有掌握抛物线,二次函数图特殊性.
知识点
13.已知函数


正确答案
4
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析