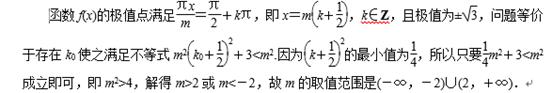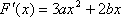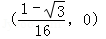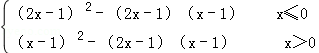- 函数与方程
- 共222题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
设函数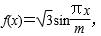
正确答案
解析
知识点
设函数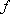
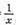

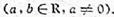
正确答案
解析
令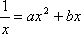
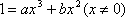

令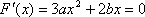
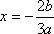

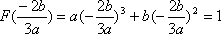
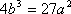
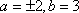

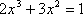
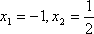
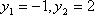
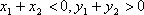
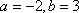
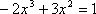


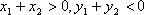
知识点
设函数
(1)设



(2)设



(3)在(1)的条件下,设



正确答案
见解析
解析
(1)

又当
(2)当n=2时,
对任意

①

②

③

综上可知,
注:②③也可合并并证明如下:
用
当
(3)证法一:设
于是有
又由(1)知
所以,数列
证法二:设

则
所以,数列
知识点
设函数fn(x)=
(1)对每个n∈N*,存在唯一的xn∈
(2)对任意p∈N*,由(1)中xn构成的数列{xn}满足0<xn-xn+p<.
正确答案
见解析
解析
(1)对每个n∈N*,当x>0时,f′n(x)=
由于f1(1)=0,当n≥2时,fn(1)=
又

所以存在唯一的xn∈
(2)当x>0时,fn+1(x)=fn(x)+
由fn+1(x)在(0,+∞)内单调递增知,xn+1<xn,故{xn}为单调递减数列,
从而对任意n,p∈N*,xn+p<xn.
对任意p∈N*,
由于fn(xn)=
fn+p(xn+p)=
①式减去②式并移项,利用0<xn+p<xn≤1,
得xn-xn+p=

因此,对任意p∈N*,都有0<xn-xn+p<
知识点
已知函数f(x)=ex,x∈R.
(1)若直线y=kx+1与f(x)的反函数的图像相切,求实数k的值;
(2)设x>0,讨论曲线y=f(x)与曲线y=mx2(m>0)公共点的个数;
(3)设a<b,比较

正确答案
(1) 



解析
(1)f(x)的反函数为g(x)=ln x.
设直线y=kx+1与g(x)=ln x的图像在P(x0,y0)处相切,
则有y0=kx0+1=ln x0,k=g′(x0)=
解得x0=e2,
(2)
曲线y=ex与y=mx2的公共点个数等于曲线
令

∴φ′(2)=0.
当x∈(0,2)时,φ′(x)<0,φ(x)在(0,2)上单调递减;
当x∈(2,+∞)时,φ′(x)>0,φ(x)在(2,+∞)上单调递增,
∴φ(x)在(0,+∞)上的最小值为
当0<m<

当

当


综上所述,当x>0时,
若0<m<
若
若
(3)解法一:可以证明
事实上,

令
则
∴ψ(x)在[0,+∞)上单调递增,
∴x>0时,ψ(x)>ψ(0)=0.
令x=b-a,即得(*)式,结论得证。
解法二:
=
=
设函数u(x)=xex+x-2ex+2(x≥0),
则u′(x)=ex+xex+1-2ex,
令h(x)=u′(x),则h′(x)=ex+ex+xex-2ex=xex≥0(仅当x=0时等号成立),
∴u′(x)单调递增,
∴当x>0时,u′(x)>u′(0)=0,
∴u(x)单调递增。
当x>0时,u(x)>u(0)=0.
令x=b-a,则得(b-a)eb-a+(b-a)-2eb-a+2>0,
∴
因此,
知识点
函数f(x)=2x|log0.5x|-1的零点个数为( )。
正确答案
解析
函数f(x)=2x|log0.5x|-1的零点也就是方程2x|log0.5x|-1=0的根,即2x|log0.5x|=1,整理得|log0.5x|=

知识点
对于实数a和b,定义运算“﹡”:a*b=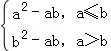
正确答案
解析
∵2x﹣1≤x﹣1时,有x≤0,
∴根据题意得f(x)=
即f(x)=
画出函数的图象从图象上观察当关于x的方程为f(x)=m(m∈R)恰有三个互不相等的实数根时,m的取值范围是(0,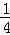
当﹣x2+x=m时,有x1x2=m,
当2x2﹣x=m时,由于直线与抛物线的交点在y轴的左边,得到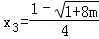
∴x1x2x3=m(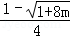
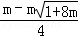
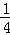
令y=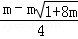
则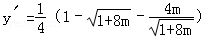
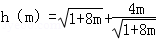
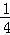
∴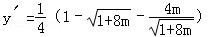
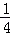
∴函数y=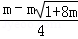
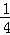
∴函数的值域是(f(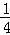
知识点
若a<b<c,则函数f(x)=(x-a)·(x-b)+(x-b)(x-c)+(x-c)(x-a)的两个零点分别位于区间( )。
正确答案
解析
由题意a<b<c,可得f(a)=(a-b)(a-c)>0,f(b)=(b-c)(b-a)<0,f(c)=(c-a)(c-b)>0.显然f(a)·f(b)<0,f(b)·f(c)<0,所以该函数在(a,b)和(b,c)上均有零点,故选A
知识点
函数
正确答案
解析
当


当


知识点
扫码查看完整答案与解析