- 等差数列的判断与证明
- 共95题
10．在等
正确答案
解析
因为
考查方向
解题思路
根据已知等式求出
易错点
在使用下标和性质时，易出错。
知识点
数列
30.求
31.求数列
32.令
正确答案
（1）
解析
考查方向
解题思路
第一问，赋值即可。第二问，利用递推公式，两个式子相减，即可得出通项公式，然后求和。第三问，利用放缩来证明。
易错点
利用递推公式求通项公式时，注意下标。
正确答案
（2）
解析
考查方向
解题思路
第二问，利用递推公式，两个式子相减，即可得出通项公式，然后求和。
易错点
利用递推公式求通项公式时，注意下标。
正确答案
（3）见解析．
解析
（3）依题由
= 
记
又
考查方向
解题思路
第三问，利用放缩来证明。
易错点
利用递推公式求通项公式时，注意下标。
6.若样本数据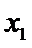
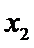
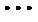
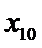
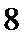
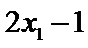
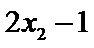
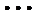
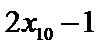
差为（ ）
A
B
C
D
正确答案
解析
设样本数据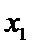
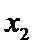
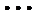
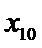
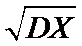
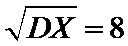
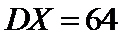
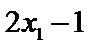
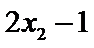
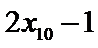
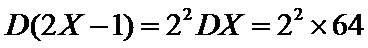
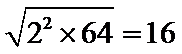
考查方向
解题思路
根据题意和相关公式分别求解。
易错点
样本的方差和标准差公式记忆错误，不理解题意
知识点
16.设Sn是数列{an}的前n项和，且a1=－1，an+1=Sn Sn+1，则Sn=________.
正确答案
知识点
8．已知非零正实数x1,x2，x3依次构成公差不为零的等差数列．设函数f(x)=x，a∈{-1，
并记M={-1，
A存在a∈M，使得f(x1)，f(x2)，f(x3)依次成等差数列
B存在a∈M，使得f(x1)，f(x2)，f(x3)依次成等比数列
C当a=2时，存在正数
D任意a∈M，都存在正数
正确答案
解析
∵当α∈M时，f（x）的变化率随x的变化而变化，∴f（x1），f（x2），f（x3）不可能成等差数列，故A错误
整理得（x1-x3）2=0，∴x1=x3．与x1，x2，x3依次构成公差不为零的等差数列相矛盾，故B错误．
当α=2时，假设f（x1），f（x2），f（x3）-λ依次成等差数列，所以λ>0,故C正确
当α＞0时，λ＞1，当α＜0时，λ＜1．故D错误．
考查方向
等比数列的性质
解题思路
由等差数列得
易错点
对等差数列的性质掌握不好，逻辑分析能力弱
知识点
扫码查看完整答案与解析