- 其它方法求和
- 共28题
已知




20.求

21.记




正确答案
(Ⅰ)
解析
试题分析:本题属于数列的基本问题,题目的难度是逐渐由易到难,(1)按照解题步骤进行求解,(2)要注意对
(Ⅰ)设公差为d,
则
由①得

由


所以

考查方向
解题思路
本题考查等差数列、等比数列、裂项抵消法求和,解题步骤如下:
1)设出公差,利用等比中项求公差;
2)利用等差数列的公式得到通项和前
3)利用裂项抵消法进行求解;
4)利用单调性求解。
易错点
1)不能准确裂项;
2)注意数列的单调性的应用.
正确答案
(Ⅱ)
解析
试题分析:本题属于数列的基本问题,题目的难度是逐渐由易到难,(1)按照解题步骤进行求解,(2)要注意对
(Ⅱ)可得
所以
由于

因为


所以实数m的取值范围是
考查方向
解题思路
本题考查等差数列、等比数列、裂项抵消法求和,解题步骤如下:
1)设出公差,利用等比中项求公差;
2)利用等差数列的公式得到通项和前
3)利用裂项抵消法进行求解;
4)利用单调性求解。
易错点
1)不能准确裂项;
2)注意数列的单调性的应用.
16.数列







正确答案
7280
解析
由






考查方向
解题思路
1.先根据



易错点
1.不会将

知识点
已知数列




17.求数列
18.设




正确答案
(1)
解析
(Ⅰ)当


当


显然当
∴
考查方向
解题思路
先令



易错点
1.不会转化题中的条件

正确答案
(2)
解析
(Ⅱ)∵
∴
考查方向
解题思路
由第(1)问的结果可以得到
易错点
不明白
已知数列








24.比较


25.证明:

正确答案
解析
由

两式相减得:

又

∴

即:
考查方向
解题思路
先由通项及数列的前n项和的关系,求出通项,再求和,进而得出数列
易错点
在利用数列的前n项和与通项的关系时,易忽略对首项的验证
正确答案
略
解析
解:由(Ⅰ)知:

因此当

则
----------------------------------11分
又∵当

当且仅当
∴
∴

考查方向
解题思路
逐级对数列{






易错点
在构造数列放缩时,放缩不合理,导致出错
已知数列



17.求数列
18.若



正确答案
an=22n-1;
解析
试题分析:本题属于等差数列通项求法与求和的应用问题,题目的难度适中。(1)求解时一定要灵活应用




(Ⅰ)由
当
当


所以数列


考查方向
解题思路
本题考查了等差数列的通项公式和求和公式的应用及性质,解题步骤如下:
由数列前



对于

易错点
由数列前


正确答案
证明略。
解析
试题分析:本题属于等差数列通项求法与求和的应用问题,题目的难度适中。(1)求解时一定要灵活应用




由(Ⅰ)可得
当
当

综上,
考查方向
解题思路
本题考查了等差数列的通项公式和求和公式的应用及性质,解题步骤如下:
由数列前



对于

易错点
由数列前


(本小题满分12分,(1)小问4分,(2)小问8分)
在数列
27.若

28.若
正确答案

解析
试题分析:(1)由于






试题解析:(1)由
若存在某个






从而


故
考查方向
解题思路
数列的问题难度大,往往表现在与递推数列有关,递推含义趋广,不仅有数列前后项的递推,更有关联数列的递推,更甚的是数列间的“复制”式递推;从递推形式上看,既有常规的线性递推,还有分式、三角、分段、积(幂)等形式.在考查通性通法的同时,突出考查思维能力、代数推理能力、分析问题解决问题的能力.
易错点
本题第(1)小题通过递推式证明数列是等比数列,从而应用等比数列的通项公式求得通项.
正确答案
证明详见解析
解析
试题分析:(2)本小题是数列与不等式的综合性问题,数列的递推关系是









试题解析:(2)由



由上式及
因为
求和得
另一方面,由上已证的不等式知
综上:
考查方向
解题思路
数列的问题难度大,往往表现在与递推数列有关,递推含义趋广,不仅有数列前后项的递推,更有关联数列的递推,更甚的是数列间的“复制”式递推;从递推形式上看,既有常规的线性递推,还有分式、三角、分段、积(幂)等形式.在考查通性通法的同时,突出考查思维能力、代数推理能力、分析问题解决问题的能力.
易错点
第(2)小题把数列与不等式结合起来,利用数列的递推式证明数列是单调数列,利用放缩法证明不等式,难度很大.
已知数列






22.分别求数列

23.若



正确答案
(1)

解析
(Ⅰ)


又因为

设等比数列

由已知

解得


所以,
考查方向
解题思路
先利用已知数列的前n项和求通项公式求出

易错点
1.不会利用数列的前n项和求通项公式;2.对于数列
正确答案
(2)
解析
(Ⅱ)
设数列





当
当


则

1-2得
所以
所以,
考查方向
解题思路
先由第(1)问得到
易错点
1.不会利用数列的前n项和求通项公式;2.对于数列
已知


17.求数列
18.求数列


正确答案
(1)
解析
(1) 设



由


考查方向
解题思路
利用等差数列的性质求出数列
易错点
利用等差数列的性质求通项公式和等比数列的性质混淆;
正确答案
解析
(2)
由
得
① -②得

又
当


考查方向
解题思路
根据公式构造等式求出
易错点
先构造等式做差后求出
11.数列




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.设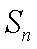
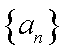
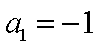
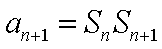
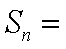
正确答案
试题分析:由已知得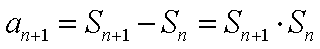
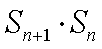
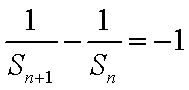
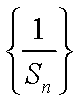
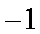
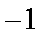
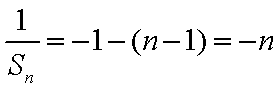
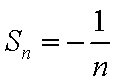
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析