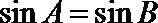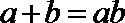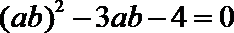- 数量积判断两个平面向量的垂直关系
- 共68题
9.向量




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.设





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.设




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.已知









正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
10.已知向量→OA=(4,6),→OB=(3,5),且→OC⊥→OA,→AC∥→OB,则向量→OC= ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 设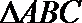
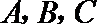
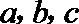
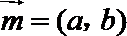
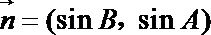
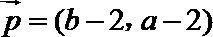
(1)若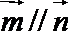
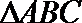
(2)若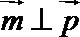
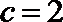
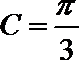
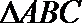
正确答案
设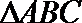
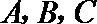

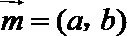
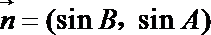
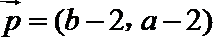
(1)若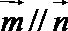
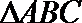
(2)若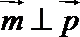
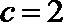
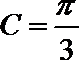
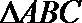
证明:(证法一)(1)∵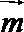
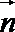
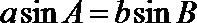
由正弦定理可知,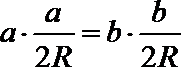
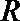
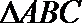
∴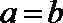

(证法二)∵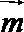
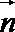
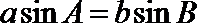
由正弦定理可知,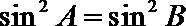
∵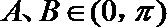
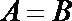
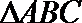
(2)由题意可知,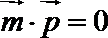
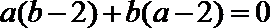
由余弦定理可知,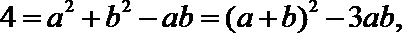


∴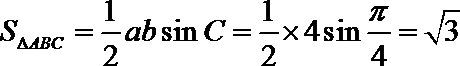
解析
解析已在路上飞奔,马上就到!
知识点
15.已知△ABC的三个内角A,B,C所对的边分别为a,b,c,向量m=(1,1-
(Ⅰ)求角B;
(Ⅱ)若a+c=b,判断△ABC的形状.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.若向量

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.已知向量


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.已知:向量


(1)若

(2)求:
正确答案
解:(1)
∵
(2)



∴当



解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析