- 数量积判断两个平面向量的垂直关系
- 共68题
13.已知向量a=(1,–1),b=(6,–4).若a⊥(ta+b),则实数t的值为________.
正确答案
-5
知识点
8.若

正确答案
解析
由



考查方向
解题思路
比较幂或对数值的大小,若幂的底数相同或对数的底数相同,通常利用指数函数或对数单调性进行比较,若底数不同,可考虑利用中间量进行比较.
易错点
指数函数和对数函数的单调性
知识点
8.已知O.A.B是平面上的三点,向量


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11. 已知平面向量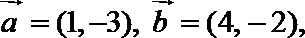
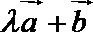
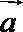
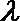
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知向量





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知向量a、b、c是同一平面内的三个向量,其中a=(1,2).
(1)若|c|=2
(2)若|b|=
正确答案
(1)令c=(x,y),则由|c|=2


又由a∥c知,2x-y=0②
联立①②可解得:

故c=(2,4)或c=(-2,-4).
(2)由a+2b与2a-b垂直知(a+2b)·(2a-b)=0,
即2a2+3a·b-2b2=0,∴a·b=
即|a||b|cosθ=

而由a=(1,2)知|a|=

∵θ∈[0,π],∴θ=π.
解析
解析已在路上飞奔,马上就到!
知识点
13.已知


正确答案
2
解析
由已知,
因为
所以
解得
应填2.
考查方向
解题思路
本题主要考查平面向量的坐标运算,向量的垂直等知识。
解题步骤如下:由向量垂直的条件,列出方程;解出方程,即得答案。
易错点
本题易把向量的平行和垂直的条件混淆,从而出现错误。
知识点
12. 已知向量



正确答案
解析
考查方向
解题思路
本题主要是突破点在于垂直与数量积之间的转换
易错点
本题注意向量垂直与数量积之间的转换
知识点
13.向量




正确答案
解析
由



考查方向
本题主要考查向量的相关知识。
解题思路
将垂直条件转化为数量积为0,代入数据求出
易错点
1.不能将垂直的条件进行转化。
2.夹角公式不清楚
知识点
15.已知圆 C : (x —3)2 + (y — 4) 2= 1 和两点 A (-m,0),B(m,0) (m>0),若圆上存在点 P,使得 ∠APB = 90°,则m的取值范围是 .
正确答案
[4,6]
解析
圆心C(3,4),半径r=1,AP垂直BP,所以(a+m)(a-m)+b2=0,即m2=a2+b2,所以OP的最大值为OC+r=5+1=6,最小值为4,所以填[4,6].
考查方向
圆的方程,两点间距离公式,最值问题。
解题思路
利用向量垂直时的数量积关系,将m转换成求OP的最大值
易错点
找不到m在圆中所代表的含义,不会运用转换思想。
知识点
扫码查看完整答案与解析