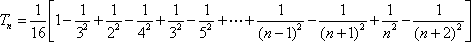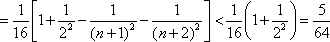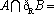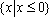- 直线与圆、圆与圆的位置关系
- 共468题
执行如图所示的程序框图,如果输出s=3,那么判断框内应填入的条件是( )
正确答案
解析
由程序框图可知,输出的结果为s=log23×log34×…×logk(k+1)=log2(k+1),由s=3,即log2(k+1)=3,解得k=7.又∵不满足判断框内的条件时才能输出s,∴条件应为k≤7
知识点
正项数列{an}的前n项和Sn满足: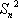
(1)求数列{an}的通项公式an;
(2)令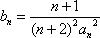
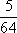
正确答案
见解析
解析
(1)解:由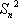
由于{an}是正项数列,所以Sn>0,Sn=n2+n.
于是a1=S1=2,n≥2时,an=Sn-Sn-1=n2+n-(n-1)2-(n-1)=2n.
综上,数列{an}的通项an=2n.
(2)证明:由于an=2n,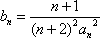
则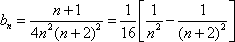
知识点
已知全集为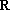
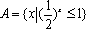
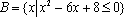
正确答案
解析
略
知识点
已知圆C1:(x-2)2+(y-3)2=1,圆C2:(x-3)2+(y-4)2=9,M,N分别是圆C1,C2上的动点,P为x轴上的动点,则|PM|+|PN|的最小值为( )。
正确答案
解析
圆C1,C2的圆心分别为C1,C2,由题意知|PM|≥|PC1|-1,|PN|≥|PC2|-3,∴|PM|+|PN|≥|PC1|+|PC2|-4,故所求值为|PC1|+|PC2|-4的最小值,又C1关于x轴对称的点为C3(2,-3),所以|PC1|+|PC2|-4的最小值为|C3C2|-4=
知识点
设{an}是有正数组成的等比数列,

正确答案
解析
由a2a4=1可得





知识点
设


正确答案
解析
约束条件对应四边形

知识点
不等式
正确答案

解析



知识点
如图,在矩形区域ABCD的A,C两点处各有一个通信基站,假设其信号的覆盖范围分别是扇形区域ADE和扇形区域CBF(该矩形区域内无其他信号来源,基站工作正常),若在该矩形区域内随机地选一地点,则该地点无信号的概率是( )。
正确答案
解析
S矩形ABCD=1×2=2,S扇形ADE=S扇形CBF=
P=
知识点
某车间共有

(1) 根据茎叶图计算样本均值;
(2) 日加工零件个数大于样本均值的工人为优秀工人.
根据茎叶图推断该车间
(3) 从该车间


正确答案
(1)22;(2)4;(3) 
解析
(1) 样本均值为
(2) 由(1)知样本中优秀工人占的比例为


(3) 设事件




知识点
某地一渔场的水质受到了污染,渔场的工作人员对水质检测后,决定往水中投放一种药剂来净化水质. 已知每投放质量为

(1)如果投放的药剂质量为m=6,试问渔场的水质达到有效净化一共可持续几天?
(2)如果投放的药剂质量为m,为了使在8天(从投放药剂算起包括第8天)之内的渔场的水质达到最佳净化,试确定应该投放的药剂质量m的取值范围。
正确答案
(1)8天;
(2)[6,9]
解析
(1)由已知得,经过x天该药剂在水中释放的浓度 y=mf(x)是关于自变量





(1)由题设:投放的药剂质量为





所以如果投放的药剂质量为
(2)由题设:


∴

∴



知识点
扫码查看完整答案与解析