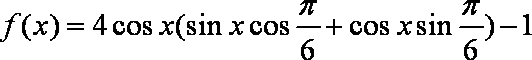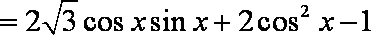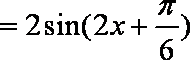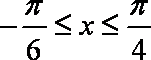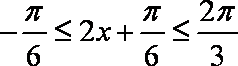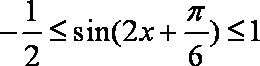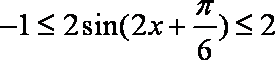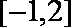- 正弦函数的定义域和值域
- 共98题
已知锐角






正确答案
见解析
解析

又





知识点
已知函数

(1)求函数
(2)当



正确答案
(1)

解析
解析:
(2)因为

函数的增区间为
知识点
在斜三角形
(1)若

(2)若

正确答案
见解析
解析
解:(1)由正弦定理,得
从而

由余弦定理,得
整理得

(2)在斜三角形

所以

即
故
整理,得
因为△ABC是斜三角形,所以sinAcosAcosC
所以
知识点
在△ABC中,设角A,B,C的对边分别为a,b,c,且
(1)求角A的大小;
(2)若
正确答案
见解析。
解析
(1)利用正弦定理化简acosC+

∵sinB=sin(A+C)=sinAcosC+cosAsinC,
∴sinAcosC+

∵sinC≠0,
∴cosA=
∵A为三角形内角,
∴A=
(2)∵a=

∴由余弦定理得:a2=b2+c2﹣2bccosA,15=16+c2﹣4c,即c2﹣4c+1=0,
解得:c=

知识点
在△









(1)求角
(2)若

正确答案
见解析。
解析
因为

所以

所以
又

(2)在

所以
由基本不等式,


所以

故

知识点
已知






(1)求
(2)当


正确答案
(1)

解析
解析:(1)因为
即

所以 
(2)由
故
由


由正弦定理,
故
知识点
已知四棱锥


(1)证明:
(2)在线段PA上是否存在一点F,使EF//平面PCD,若存在,求
正确答案
见解析。
解析
(1)证明:平面ABCD,CD

因为ABCD为直角梯形,且AB=BC=1,
易知四边形ABCM为矩形,所以AC=CD=


又

PC

(2)





取AM的中点G,则GE为

又因为四边形ABCM为矩形,所以

因为






即,当


知识点
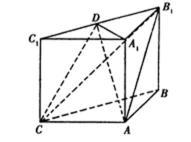
如图,三棱柱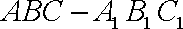
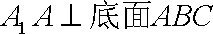
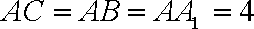

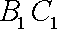
(1)求证: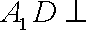
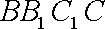
(2)求三棱锥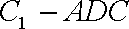
正确答案
见解析
解析
(1)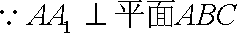
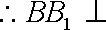
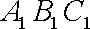
又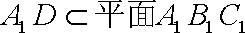
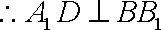
又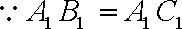
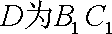
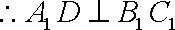
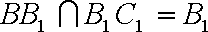
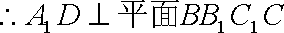
(2):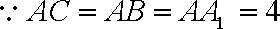
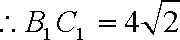
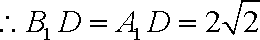
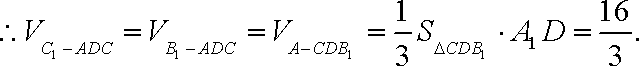
知识点
已知函数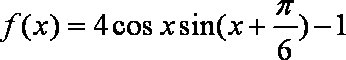
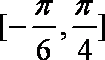
正确答案
见解析。
解析
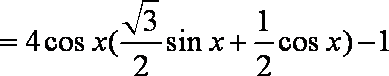
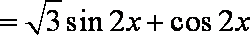
∵
∴
∴
所以,函数在区间的值域是
知识点
在






(1)求
(2)求
正确答案
见解析。
解析
(1)由已知



由余弦定理可得

(2)由(1)知

所以
知识点
扫码查看完整答案与解析