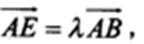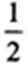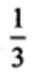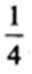正弦函数的定义域和值域
共98题

· 正弦函数的定义域和值域

正弦函数的定义域和值域
共98题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

设与是定义在同一区间[a, b]上的两个函数，若函数上有两个不同的零点，则称和在[a, b]上是“联系函数”，区间[a, b]称为“联系区间”，若与在[0,3]上是“联系函数”，则k的取值范围为 ( )

正确答案

解析

依题意，令，则在上有两个零点，所以，即，则有

知识点

正弦函数的定义域和值域

题型：简答题

简答题 · 16 分

将圆按向量平移得到圆，直线与圆相交于、

两点，若在圆上存在点，使求直线的方程。

正确答案

见解析。

解析

由已知圆的方程为，

按平移得到.

∵∴.

即.

又，且，∴.∴.

设，的中点为D.

由，则，又.

∴到的距离等于.

即， ∴m=1

∴直线的方程为：或.

知识点

正弦函数的定义域和值域

题型：单选题

单选题 · 5 分

已知△ABC中，D是BC边的中点，过点D的直线分别交直线AB、AC于点E、F，若

的最小值是

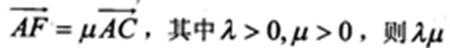
正确答案

解析

解析：由已知得：，,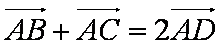

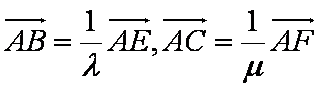
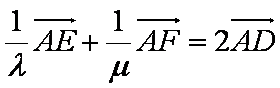
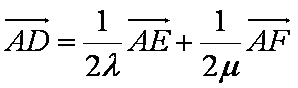
所以,即,

因为D,E,F三点共线，

所以，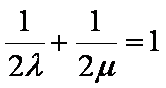

又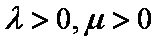，由基本不等式可得：

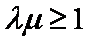
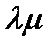
所以，即的最小值是1，

知识点

正弦函数的定义域和值域

题型：简答题

简答题 · 13 分

已知函数(R )。

（1）求函数的最小正周期及单调递增区间；

（2）内角的对边长分别为，若且

试判断的形状，并说明理由。

正确答案

见解析

解析

（1）∵，

∴.故函数的最小正周期为；递增区间为(Z )

（2）解法一：，∴，

∵，∴，∴，即，

由余弦定理得：，∴，即，

故（不合题意，舍）或。

因为，所以ABC为直角三角形.

解法二：，∴。

∵，∴，∴，即，

由正弦定理得：，∴，

∵，∴或，当时，；当时，，（不合题意，舍）所以ABC为直角三角形.

知识点

正弦函数的定义域和值域

题型：单选题

单选题 · 5 分

已知点为的外心，且，，则( )。

正确答案

解析

取一个Rt△ABC,使斜边为|AC|=4 ,|AB|=2,则6.

知识点

正弦函数的定义域和值域

题型：填空题

填空题 · 5 分

若斜率互为相反数且相交于点的两条直线被圆：所截得的弦长之比为，则这两条直线的斜率之积为 ▲ 。

正确答案

-9或

解析

略

知识点

正弦函数的定义域和值域

题型：简答题

简答题 · 10 分

直线（极轴与x轴的非负半轴重合，且单位长度相同）。

（1）求圆心C到直线的距离；

（2）若直线被圆C截的弦长为的值。

正确答案

见解析。

解析

（1）把化为普通方程为

把化为直角坐标系中的方程为

圆心到直线的距离为

（2）由已知

，

知识点

正弦函数的定义域和值域

题型：单选题

单选题 · 5 分

若函数（ω>0）在区间上单调递增，在区间上单调递减，则ω=（）

正确答案

解析

函数的周期,因为在区间上单调递增，在区间上单调递减,所以,.简单考查三角函数的图像和单调性,周期问题,是简单题.

知识点

正弦函数的定义域和值域

题型：简答题

简答题 · 8 分

已知，函数

（1）求的最小正周期，并求其图象对称中心的坐标；

（2）当时，求函数f(x)的值域.

正确答案

见解析。

解析

（1）

………2分

所以的最小正周期为

令，得。

故所求对称中心的坐标为- ………4分

（2） ………6分

即的值域为　　 - ………8分

知识点

三角函数的周期性及其求法正弦函数的定义域和值域正弦函数的对称性三角函数中的恒等变换应用数量积的坐标表达式

题型：简答题

简答题 · 12 分

某网站就观众对2010年春晚小品类节目的喜爱程度进行网上调查，其中持各种态度的人数如下表：

（1）现用分层抽样的方法从所有参与网上调查的观众中抽取了一个容量为n的样本，已知从不喜欢小品的观众中抽取的人数为5人，则n的值为多少？

（2）在（1）的条件下，若抽取到的5名不喜欢小品的观众中有2名为女性，现将抽取到的5名不喜欢小品的观众看成一个总体，从中任选两名观众，求至少有一名为女性观众的概率.

正确答案

见解析。

解析

（1）采有分层抽样的方法，样本容量与总体容量的比为

则不喜爱小品观众应抽取人

（2）由题意得，女性观众抽取2人，男性观众抽取3人，

设女性观众为，男性观众为

则从5位不喜爱小品的观众中抽取两名观众有10种可能：

其中抽取两名观众中至少有一名为女性观众有7种可能：

所以从5位不喜爱小品的观众中抽取两名观众，至少有一名为女性观众的概率为

知识点

正弦函数的定义域和值域

继续学习学习下一知识点

下一知识点 : 正弦函数的单调性

百度题库 > 高考 > 文科数学 > 正弦函数的定义域和值域

扫码查看完整答案与解析