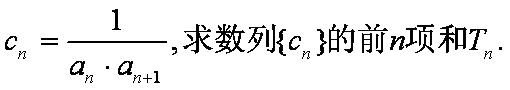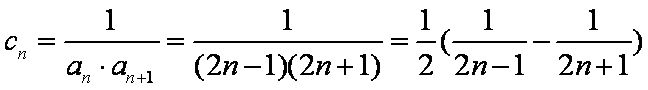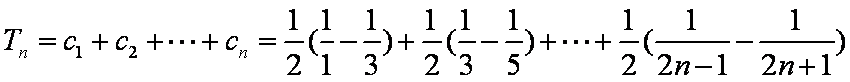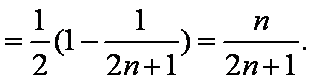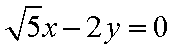正弦函数的定义域和值域
共98题

· 正弦函数的定义域和值域

正弦函数的定义域和值域
共98题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

若，则

正确答案

解析

由已知. 故选C.

知识点

正弦函数的定义域和值域

题型：简答题

简答题 · 13 分

已知等差数列

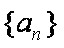
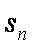
（1）求数列的通项公式，写出它的前n项和；

（2）求数列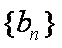的通项公式；

（3）若

正确答案

见解析。

解析

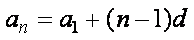
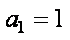
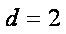
（1）设，由题意得，，

所以，；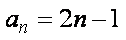

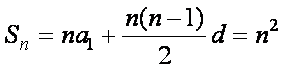
（2），，所以，，…… （）

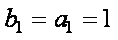
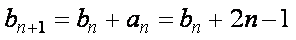
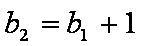
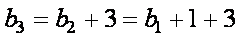
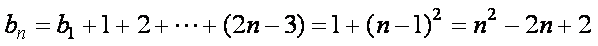
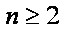
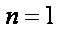
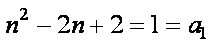
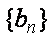
又时，所以数列的通项；

（3）

知识点

正弦函数的定义域和值域

题型：简答题

简答题 · 10 分

定义的最大值。

正确答案

见解析。

解析

当时，恒成立；

当时，在恒成立；

当时，恒成立；

所以，

当时，；当时，；当时，。

综上：最大值为5。

知识点

正弦函数的定义域和值域

题型：简答题

简答题 · 12 分

函数的部分图像如图所示.

（1）求函数的解析式；

（2）当时，求的取值范围。

正确答案

（1）

（2）[-1,]

解析

（1）由图像得，，所以，则；将代入得，而，所以，因此函数； (6分)

（2）由于，，所以，所以的取值范围是. ( 12分)

知识点

正弦函数的定义域和值域由y=Asin（ωx+φ）的部分图象确定其解析式

题型：简答题

简答题 · 13 分

已知椭圆C的标准方程为：+=1（a＞b＞0），该椭圆经过点P（1，），且离心率为。

（1）求椭圆的标准方程；

（2）过椭圆：+=1（a＞b＞0）长轴上任意一点S（s，0），（﹣a＜s＜a）作两条互相垂直的弦AB、CD，若弦AB、CD的中点分别为M、N，证明：直线MN恒过定点。

正确答案

见解析。

解析

（1）∵点在椭圆上，

又，解得，

∴椭圆方程为

（2）设直线AB的方程为，则直线CD的方程为

联立可得

设

由中点坐标公式得

将M的坐标中的用代换，得CD的中点

∴直线MN的方程为

令得：，所以直线MN经过定点

当时，易知直线MN也经过定点.

综上所述，直线MN经过定点

知识点

正弦函数的定义域和值域

题型：填空题

填空题 · 4 分

已知是椭圆和双曲线的公共焦点，是它们的一个公共点，且，则的最大值为

正确答案

解析

略

知识点

正弦函数的定义域和值域

题型：单选题

单选题 · 5 分

已知是定义在上的函数，下列命题正确的是 ( )

A若在区间上的图像是一条连续不断的曲线，且在内有零点，则有.

B若在区间上的图像是一条连续不断的曲线，且有，则其在内没有零点。

C若在区间上的图像是一条连续不断的曲线，且有，则其在内有零点。

D如果函数在区间上的图像是一条连续不断的曲线，且有，则其在区间内有零点。

正确答案

解析

略

知识点

正弦函数的定义域和值域

题型：填空题

填空题 · 5 分

在△ABC中，AC边上的高为BD，垂足为D，且||=，则•=　　。

正确答案

-3

解析

∵BD是AC边上的高，∴BD丄AC，

∴=0，

∵||=，

∴•=•（+）=•+•=0﹣2=﹣3。

故答案为：﹣3，

知识点

正弦函数的定义域和值域

题型：简答题

简答题 · 13 分

函数f（x）=x2（0＜x＜1）的图象如图所示，其在点M（t，f（t））处的切线为l，l与x轴和直线x=1分别交于点P、Q，点N（1，0），设△PQN的面积为S=g（t）。

（1）求g（t）的表达式；

（2）若△PQN的面积为b时的点M恰好有两个，求b的取值范围。

正确答案

见解析。

解析

（1）由条件，，于是切线的斜率为，于是的方程为，则点。

所以。

（2），当时，，单调递增；

当时，，单调递减。

又

要使的面积为时的点恰好有两个，则必有.

知识点

正弦函数的定义域和值域

题型：简答题

简答题 · 14 分

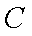
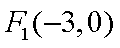
已知中心在原点的双曲线的一个焦点是，一条渐近线的方程是

（1）求双曲线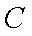的方程；

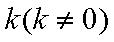
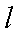
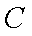
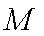
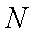
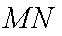
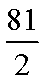
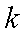
（2）若以为斜率的直线与双曲线相交于两个不同的点，，且线段的垂直平分线与两坐标轴围成的三角形的面积为，求的取值范围

正确答案

见解析

解析

（1）设双曲线的方程为， 1分

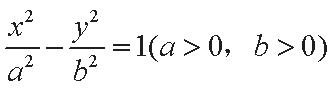
由题设得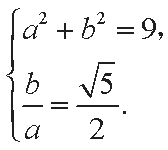 3分

解得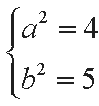， 5分

所以双曲线的方程为； 6分

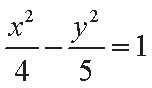
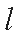
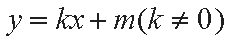
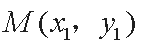
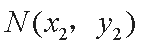
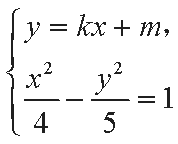
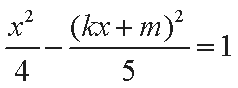
（2）设直线的方程为，点，的坐标满足方程组，将①式代入②式，得，

整理得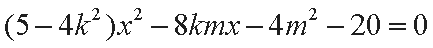， 8分

此方程有两个不等实根，于是，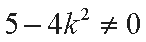

且，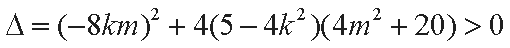

整理得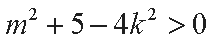，③ 9分

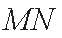
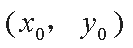
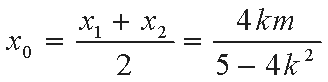
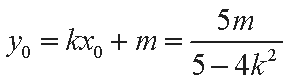
由根与系数的关系可知线段的中点坐标满足：

，， 10分

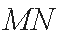
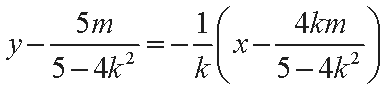
从而线段的垂直平分线的方程为， 1分

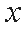
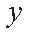
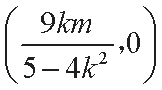
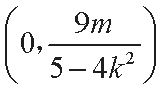
此直线与轴，轴的交点坐标分别为，，

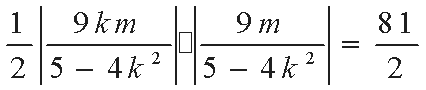
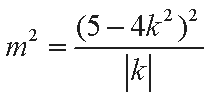
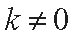
由题设可得，整理得，， 12分

将上式代入③式得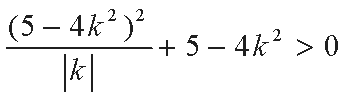， 13分

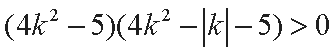
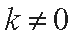
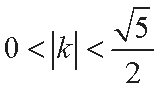
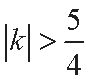
整理得，，解得或，

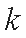
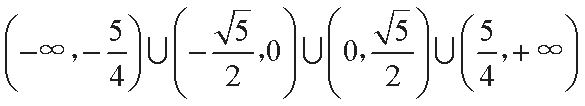
所以的取值范围是， 14分

知识点

正弦函数的定义域和值域

继续学习学习下一知识点

下一知识点 : 正弦函数的单调性

百度题库 > 高考 > 文科数学 > 正弦函数的定义域和值域

扫码查看完整答案与解析