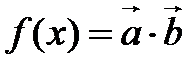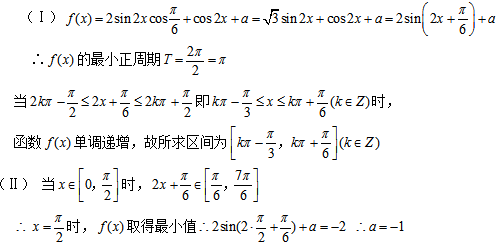- 正弦函数的定义域和值域
- 共98题
3.命题“∀x∈R,x2+x≥2”的否定是( )
正确答案
解析
略
知识点
13. 若等边




正确答案
-2
解析
略
知识点
16.已知向量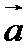
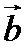
(1)求f (x)的最小正周期;
(2)求f(x)在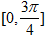
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知函数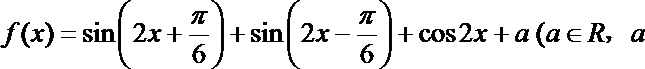
(Ⅰ)求函数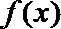
(Ⅱ)当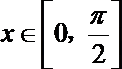
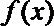
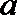
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知:函数




(1)求:
(2)当

正确答案
解:(1)由最低点为

由





由点


∵

∴
(2)∵

当



当


故

解析
解析已在路上飞奔,马上就到!
知识点
12.连掷两颗骰子得到的点数分别记为





正确答案
解析




















知识点
21.已知函数

(1)求
(2)若
(Ⅰ)证明:当


(Ⅱ)证明不等式
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知:函数



(1)求:
(2)当

正确答案
(1)由最高点为


由点

所以
又


(2)因为
所以当
解析
解析已在路上飞奔,马上就到!
知识点
19.如图,在三棱锥





(Ⅰ)求证:DE⊥平面
(Ⅱ)若PC⊥AD,且三棱锥
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析