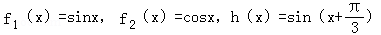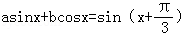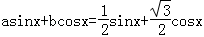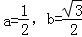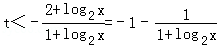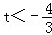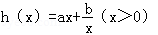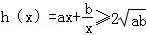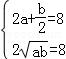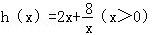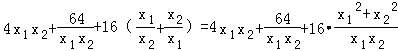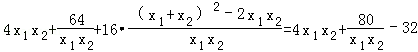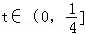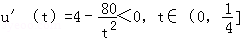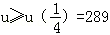- 正弦函数的定义域和值域
- 共98题
18.已知函数
(Ⅰ)求
(Ⅱ)设

正确答案
(Ⅰ)∵


(Ⅱ)∵









故
解析
解析已在路上飞奔,马上就到!
知识点
23.对于函数f1(x),f2(x),h(x),如果存在实数a,b使得h(x)=a•f1(x)+b•f2(x),那么称h(x)为f1(x),f2(x)的生成函数。
(1)下面给出两组函数,h(x)是否分别为f1(x),f2(x)的生成函数?并说明理由。
第一组:
第二组:f1(x)=x2﹣x,f2(x)=x2+x+1,h(x)=x2﹣x+1
(2)设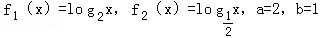
(3)设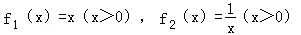
正确答案
解:(1)①设
即
取
所以h(x)是f1(x),f2(x)的生成函数
②设a(x2+x)+b(x2+x+1)=x2﹣x+1
即(a+b)x2+(a+b)x+b=x2﹣x+1
则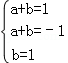
所以h(x)不是f1(x),f2(x)的生成函数
(2)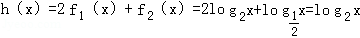
即log2(4x)+t•log2(2x)<0
所以,(2+log2x)+t(1+log2x)<0
因为x∈[2,4],所以1+log2x∈[2,3]
则
函数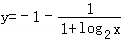
所以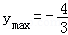
故
(3)由题意得,
则
故
解得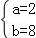
假设存在最大的常数m,使h(x1)h(x2)≥m恒成立
于是设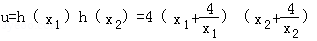
=
设t=x1x2,
则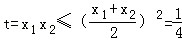
即
设
因为
所以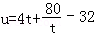
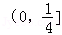
从而
故存在最大的常数m=289
解析
解析已在路上飞奔,马上就到!
知识点
15.已知函数
(1)求函数
(2)若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数
(1)求f(x)的最小正周期;
(2)求函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.函数
(1)求函数的最小正周期;
(2)求函数解析式;
(3)当
正确答案
(1)16
(2)
(3)
解析
解析已在路上飞奔,马上就到!
知识点
19. 已知函数
(Ⅰ)求函数

(Ⅱ)若对于任意的


正确答案
(Ⅰ)

∵


∴


(Ⅱ)∵对于任意的

∴


解得

解析
解析已在路上飞奔,马上就到!
知识点
16.已知向量m=(sin x,1),n=(Acos x,cos 2x) (A>0),函数f(x)=m·n的最大值为6.
(1)求A的值;
(2)将函数y=f(x)的图象向左平移个单位,再将所得图象上各点的横坐标缩短为原来的倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)在
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.设函数
(Ⅰ)求
(Ⅱ)当

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.已知函数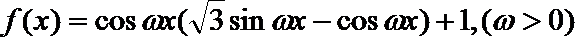
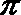
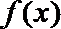
正确答案
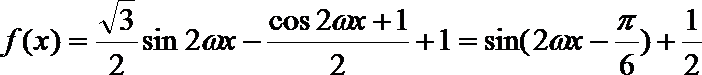
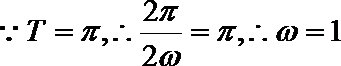
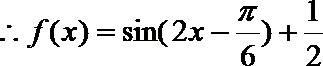
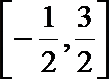
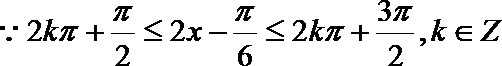
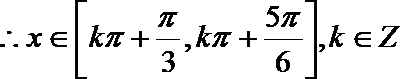
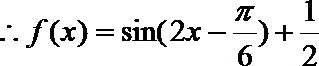
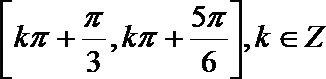
解析
解析已在路上飞奔,马上就到!
知识点
18.已知a=(sin2x,2cos2x-1),b=(sin




(Ⅰ)求
(Ⅱ)当x∈
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析