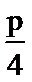- 正弦函数的定义域和值域
- 共98题
15.（本小题满分14分）
在
（1）求AB的长；
（2）求
正确答案
知识点
6.若tanθ=
A
B
C
D
正确答案
知识点
11.在封闭的直三棱柱ABC－A1B1C1内有一个体积为V的球。若AB⊥BC，AB=6，BC=8，AA1=3，则V的最大值是（）
A
B
C
D
正确答案
知识点
7.已知△ABC是边长为1的等边三角形，点
A
B
C
D
正确答案
知识点
1．设集合
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
11 ．有一个几何体的正视、侧视、俯视图分别如下，则该几何体的表面积为 （ ）
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
15．已知函数
（I）求函数
（Ⅱ）若
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
14．已知函数
且
则
正确答案
8
解析
结合正弦函数
欲
故按如下图所示取点符合要求,
即
此时
因
结合
故其总和达不到12.
故
知识点
在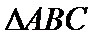
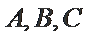
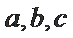
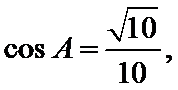
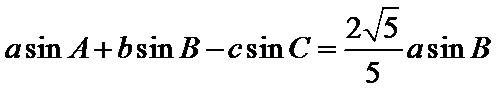
17. 求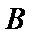
18. 设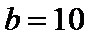
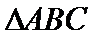
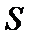
正确答案
解析
试题分析：本题属于解三角形的问题，（1）考查正余弦定理的综合应用，（2）考查正弦定理和三角形的面积公式。
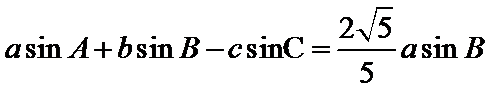
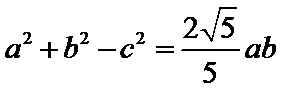
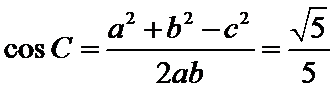
又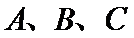
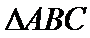
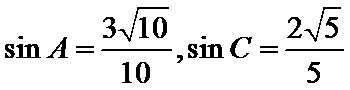
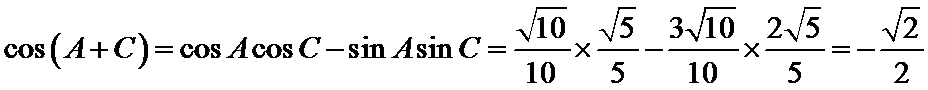
又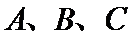
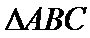
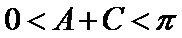
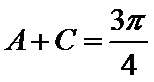
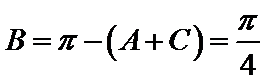
考查方向
解题思路
（1）根据正弦定理实现边角互化，然后用余弦定理求出角C的三角函数值，再进一步求出角B的三角函数值，最终确定角B的大小，
（2）由正弦定理求出c边，然后利用三角形的面积公式即可解出答案。
易错点
不知道用正弦定理实现边角互化。
正确答案
60
解析
试题分析：本题属于解三角形的问题，（1）考查正余弦定理的综合应用，（2）考查正弦定理和三角形的面积公式。
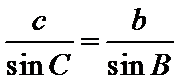
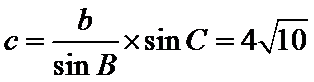
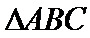
考查方向
解题思路
（1）根据正弦定理实现边角互化，然后用余弦定理求出角C的三角函数值，再进一步求出角B的三角函数值，最终确定角B的大小，
（2）由正弦定理求出c边，然后利用三角形的面积公式即可解出答案。
易错点
不知道用正弦定理实现边角互化。
14．函数
正确答案
解析
化简得
考查方向
解题思路
再利用三角变换将函数化为一个角一个三角函数，再利用图像或性质
易错点
误用公式。
知识点
扫码查看完整答案与解析