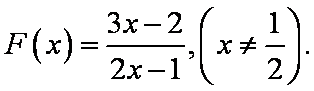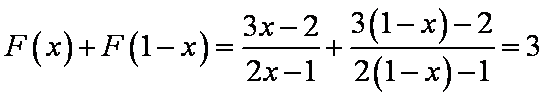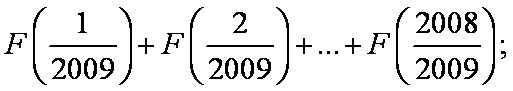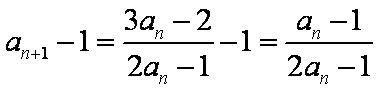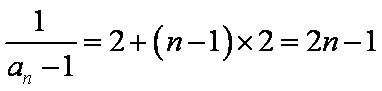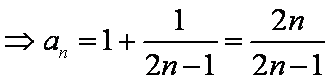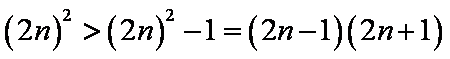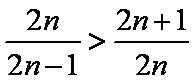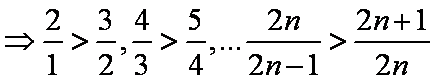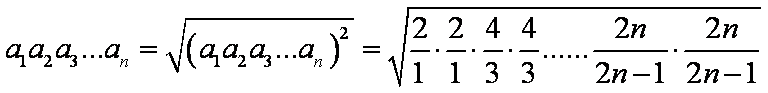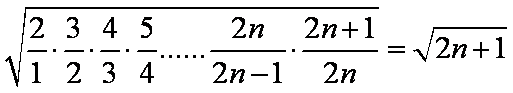- 导数与积分
- 共3028题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
已知函数
(1)若a=2,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)求f(x)在区间[2,3]上的最大值和最小值。
正确答案
见解析
解析
(1)解:f(x)的定义域为R,且 f'(x)=2x2﹣4x+2﹣a,当a=2时,
所以曲线y=f(x)在点(1,f(1))处的切线方程为 
(2)解:方程f'(x)=0的判别式为△=(﹣4)2﹣4×2×(2﹣a)=8a。
1)当a≤0时,f'(x)≥0,所以f(x)在区间(2,3)上单调递增,所以f(x)在区间[2,3]
上的最小值是
2)当a>0时,令f'(x)=0,得 

故f(x)的单调增区间为


①当0<a≤2时,x2≤2,此时f(x)在区间(2,3)上单调递增,所以f(x)在区间[2,3]
上的最小值是
②当2<a<8时,x1<2<x2<3,此时f(x)在区间(2,x2)上单调递减,在区间(x2,3)上单调递增,
所以f(x)在区间[2,3]上的最小值是 
因为 
所以 当


③当a≥8时,x1<2<3≤x2,此时f(x)在区间(2,3)上单调递减,
所以f(x)在区间[2,3]上的最小值是f(3)=7﹣3a;最大值是
综上可得,
当a≤2时,f(x)在区间[2,3]上的最小值是
当

当


当a≥8时,f(x)在区间[2,3]上的最小值是7﹣3a,最大值是
知识点
在







(1)若


(2)设

正确答案
(1)4
(2)
解析
(1)因为
所以
因为
所以
因为


所以
所以

(2)因为
所以

因为
所以
所以当



知识点
已知函数
(1)求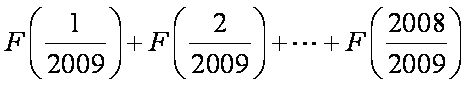
(2)已知数列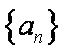
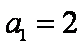
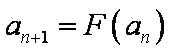
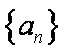
(3) 求证: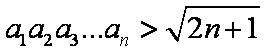
正确答案
见解析
解析
解析:(1)因为
所以设S=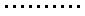
S=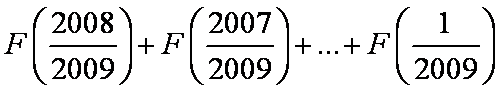
(1)+(2)得:
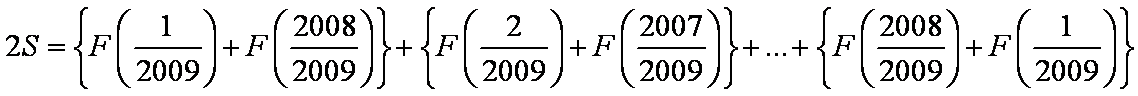
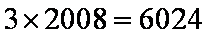
(2)由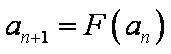
所以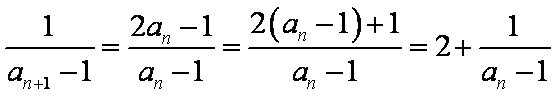
所以
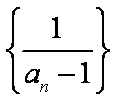

所以
(3)因为
所以
所以
>
知识点
设

(1)当

(2)若


正确答案
(1)

解析
对

(1)当


结合①,可知
所以,

(2)若

在R上恒成立,因此

知识点
函数
正确答案
解析
略
知识点
已知点


①
②当

③
④当




其中,所有正确说法的序号是 .
正确答案
③④
解析
略
知识点
给一个正方体的六个面涂上四种不同颜色(红、黄、绿、兰),要求相邻两个面涂不同的颜色,则共有涂色方法(涂色后,任意翻转正方体,能使正方体各面颜色一致,我们认为是同一种涂色方法( )
正确答案
解析
解:由于涂色过程中,要保证满足用四种颜色,且相邻的面不同色,对于正方体的三对面来说,必然有两对同色,一对不同色,而且三对面具有“地位对等性”,因此,只需从四种颜色中选择2种涂在其中两对面上,剩下的两种颜色涂在另外两个面即可,因此共有
故选A。
知识点
设



正确答案
解析
画出可行域,可知



知识点
设函数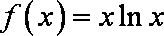
(1)求函数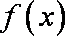
(2)设
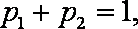
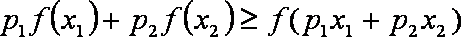
(3)设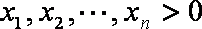
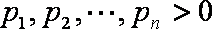
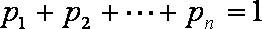
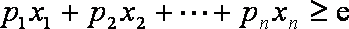
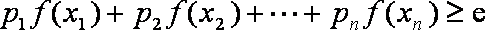
正确答案
见解析
解析
(1)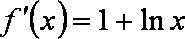
由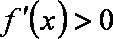
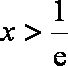
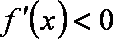
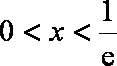
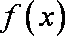
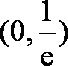
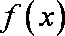
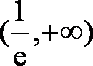
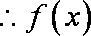
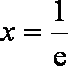
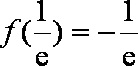
(2)令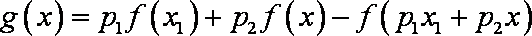
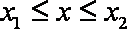
则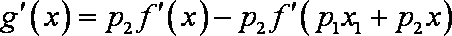
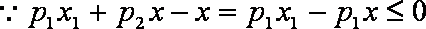
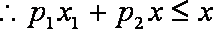
而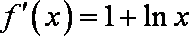
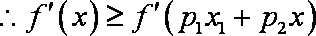
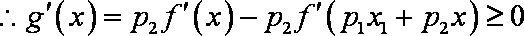
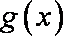
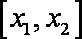
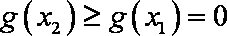
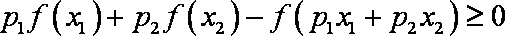
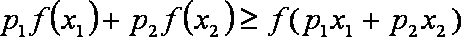
(3)先证明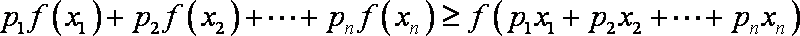
当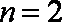
假设当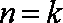
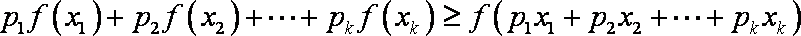
当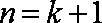
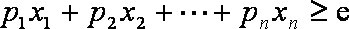
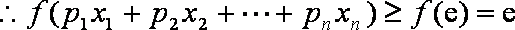
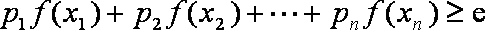
知识点
扫码查看完整答案与解析