- 导数与积分
- 共3028题
某地区对12岁儿童瞬时记忆能力进行调查,瞬时记忆能力包括听觉记忆能力与视觉记忆能力.某班学生共有40人,下表为该班学生瞬时记忆能力的调查结果,例如表中听觉记忆能力为中等,且视觉记忆能力偏高的学生为3人。
由于部分数据丢失,只知道从这40位学生中随机抽取一个,视觉记忆能力恰为中等,且听觉记忆能力为中等或中等以上的概率为
(1)试确定

(2)从40人中任意抽取3人,求其中至少有一位具有听觉记忆能力或视觉记忆能力超常的学生的概率;
(3)从40人中任意抽取3人,设具有听觉记忆能力或视觉记忆能力偏高或超常的学生人数为


正确答案
(1)a=6,b=2(2)
解析
(1)由表格数据可知,视觉记忆能力恰为中等,且听觉记忆能力为中等或中等以上的学生共有

则

所以
答:

(2)由表格数据可知,具有听觉记忆能力或视觉记忆能力超常的学生共有8人。
方法1:记“至少有一位具有听觉记忆能力或视觉记忆能力超常的学生”为事件
则“没有一位具有听觉记忆能力或视觉记忆能力超常的学生”为事件
所以
答:从这40人中任意抽取3人,其中至少有一位具有听觉记忆能力或视觉记忆能力超常的学生的概率为
方法2:记“至少有一位具有听觉记忆能力或视觉记忆能力超常的学生”为事件
所以
答:从这40人中任意抽取3人,其中至少有一位具有听觉记忆能力或视觉记忆能力超常的学生的概率为
(3)由于从40位学生中任意抽取3位的结果数为


所以从40位学生中任意抽取3位,其中恰有



因为



所以
所以
答:随机变量

知识点
如图,在边长为π的正方形内的正弦曲线
正确答案
解析
区域M的面积为:SM=



知识点
若函数


正确答案
解析
由图知,

∴


解得
知识点
对某校高一年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数,根据此数据作出了频数与频率的统计表和频率分布直方图如下:
(1)求出表中M、P及图中a的值;
(2)若该校高一学生有360人,试估计他们参加社区服务的次数在区间[15,20)内的人数;
(3)学校决定对参加社区服务的学生进行表彰,对参加活动次数在[25,30)区间的学生发放价值80元的学习用品,对参加活动次数在


正确答案
见解析。
解析
(1)由题可知 


又
解得 


则

(2)由(1)知,参加服务次数在区间

(3)所取出两人所获得学习用品价值之差的绝对值可能为0元、20元、40元、60元,则




所以


知识点
设函数
(1) 判断

(2) 若不等式




(3)设





正确答案
见解析
解析
解析:(1)∵ 

设


∴




∴


(2)①∵











②显然当

当


下面证明一个更强的不等式:

即



由(1) 知



∴不等式②成立,从而①成立 又
∴
综合上面∴





知识点
如图,圆
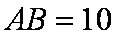
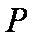
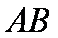
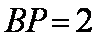
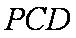


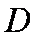
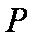
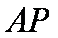
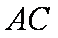
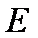

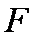
(1)求证: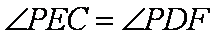
(2)求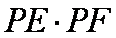
正确答案
见解析
解析
解法1:(1)连接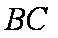
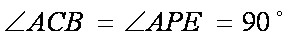
即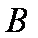
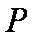
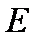

∴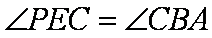
又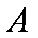
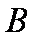

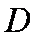
∴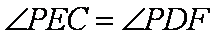
∵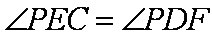
∴

∴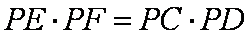
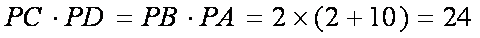
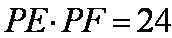
解法2:(1)连接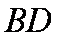
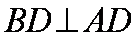
∴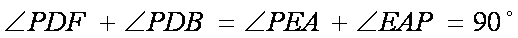
∵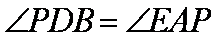
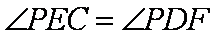
(2)∵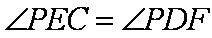
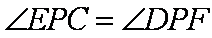
∴
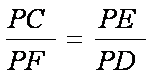
即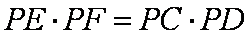
又∵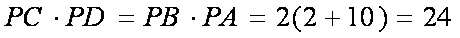
∴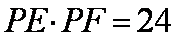
知识点
已知数列
(1)求
(2)已知存在实数



(3)记




正确答案
见解析
解析
解析:(1)




(2)
=
=




由题意,令

(3)由(2)知
所以
此时
=

>
知识点
已知不等式



正确答案
见解析。
解析
因为

又


解得
知识点




正确答案
3或
解析
由二项式定理可知



知识点
如图,焦距为2的椭圆E的两个顶点分别为



(1)求椭圆E的标准方程;
(2)若直线
正确答案
(1)
解析
(1)设椭圆E的标准方程为






∴

(2)设


消去y,得,
∴


∵原点O总在以PQ为直径的圆内,∴

又
由


故实数m的取值范围是
知识点
扫码查看完整答案与解析