- 导数与积分
- 共3028题
13.已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.曲线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.设函数

(1)求a,b的值;
(2)证明:
正确答案
由题设,y=f(x)在点P(1,0)处切线的斜率为2.
∴
因此实数a,b的值分别为-1和3.
(2)证明 f(x)=x-x2+3ln x(x>0).
设g(x)=f(x)-(2x-2)=2-x-x2+3ln x,
则g′(x)=-1-2x+

当0<x<1时,g′(x)>0;当x>1时,g′(x)<0.
∴g(x)在 (0,1)上单调递增;在(1,+∞)上单调递减.
∴g(x)在x=1处有最大值g(1)=0,
∴f(x)-(2x-2)≤0,即f(x)≤2x-2,得证
解析
解析已在路上飞奔,马上就到!
知识点
15.抛物线


正确答案
解析
知识点
20.已知函数




(Ⅰ)求a的值;
(Ⅱ)是否存在k的值,使直线
(Ⅲ)如果对于所有

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知曲线y=3x2+2x在点(1,5)处的切线与直线2ax-y-6=0平行,则a=( ).
正确答案
4
解析
解析已在路上飞奔,马上就到!
知识点
15.已知点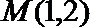
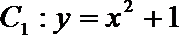
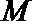
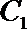
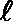
(1)求切线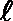
(2)把函数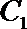
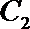
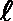
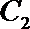
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.某公园草坪上有一扇形小径(如图),扇形半径为















(1)当

(2)函数

(3)若

(4)

其中正确的判断序号是( )(把你认为正确的判断序号都填上)。
正确答案
(2).(3).(4)
解析
解析已在路上飞奔,马上就到!
知识点
15.点P在曲线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析