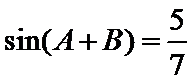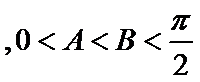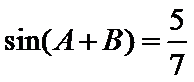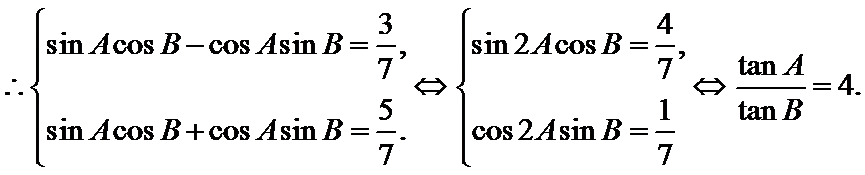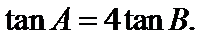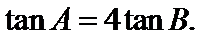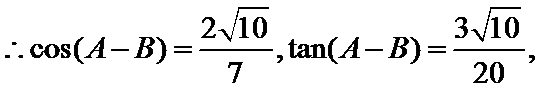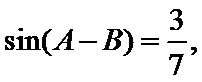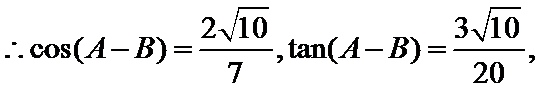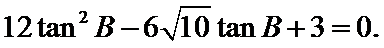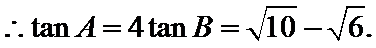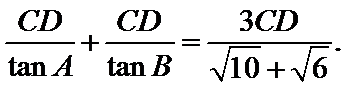- 导数与积分
- 共3028题
5.函数y=
正确答案
[-3,1]
知识点
14.设抛物线


正确答案
解析
抛物线的普通方程为














考查方向
解题思路
先求出抛物线的普通方程,再根据面积求p的值.
易错点
解题时一定要注意运算的准确性与技巧性,基础题失分过多是相当一部分学生数学考不好的主要原因。
知识点
设函数

26.求
27. 若




28.设




正确答案




解析
本题属于导数的综合应用问题,属于拔高题,不容易得分,解析如下:
(Ⅰ)解:由

下面分两种情况讨论:
(1)当



(2)当



当


所以



考查方向
解题思路
(Ⅰ)先求函数的导数:






易错点
第二问不知如何就参数的范围进行讨论导致失分。
正确答案
(Ⅱ)证明:因为




进而
又






解析
本题属于导数的综合应用问题,属于拔高题,不容易得分,解析如下:
(Ⅱ)证明:因为




进而
又






考查方向
解题思路
(Ⅱ)由题意得


易错点
第二问不知如何就参数的范围进行讨论导致失分。
正确答案
(Ⅲ





使得
当




当
∵
∴
若

当

综上所述,当



解析
本题属于导数的综合应用问题,属于拔高题,不容易得分,解析如下:
(Ⅲ





使得
当




当
∵
∴
若

当

综上所述,当



考查方向
解题思路
(Ⅲ)实质研究函数








易错点
第二问不知如何就参数的范围进行讨论导致失分。
22.(本题满分16分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分6分.
已知

(1)当

(2)若关于


(3)设




正确答案
知识点
15.在平面直角坐标系中,当P(x,y)不是原点时,定义P的“伴随点”为
当P是原点时,定义P的“伴随点“为它自身,平面曲线C上所有点的“伴随点”所构成的曲线
①若点A的“伴随点”是点

②单位圆的“伴随曲线”是它自身;
③若曲线C关于x轴对称,则其“伴随曲线”
④一条直线的“伴随曲线”是一条直线.
其中的真命题是_____________(写出所有真命题的序列).
正确答案
知识点
设

其中
(Ⅰ)求使得等式
(Ⅱ)(i)求
(ii)求

正确答案
(I)由于
当

当

所以,使得等式


(II)(i)设函数



所以,由


(ii)当

当

所以,
知识点
12.定义“规范01数列”{an}如下:{an}共有2m项,其中m项为0,m项为1,且对任意

正确答案
解析
由题意,得必有

考查方向
解题思路
将所有规范01数列列表,根据表格找出适合条件的数列。
易错点
注意列表的规范性,避免重复与遗漏。
知识点
.设
18.求
19.把



正确答案
(1)[-


解析
(Ⅰ)f(x)=2
=2



=

=sin2x-

=2(


=2sin(2x-

-






所以单调递增区间为[-


考查方向
解题思路
化简函数并计算即可得出函数的单调区间
易错点
三角恒等变换中公式的特点、符号、以及变形应用,三角函数图像变换的途径分析。
正确答案
(2)
解析
(Ⅱ)经变换g(x)=2 sinx+

考查方向
解题思路
函数平移计算
易错点
三角恒等变换中公式的特点、符号、以及变形应用,三角函数图像变换的途径分析。
20. 已知函数

(Ⅰ)若函数



(Ⅱ)若直线


(Ⅲ)当











正确答案
(1)

解析
试题分析:本题属于导数应用中的基本问题,题目的难度是逐渐由易到难,(1)直接按照步骤来求;(2)要注意对参数的讨论.
(Ⅰ) 


∵



即对



故实数

(Ⅱ) 设切点

即

令

令

当



当



∴


(Ⅲ)由题意知

两式相加得

即
∴
即
不妨令

令

∴


∴


又
∴

令




又
∴
则
即
考查方向
解题思路
本题考查导数的性质,解题步骤如下:1、求导,然后解导数不等式,求单调区间。2、对参数分类讨论求得零点个数。
易错点
第二问中的易丢对a的分类讨论。
知识点
已知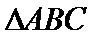
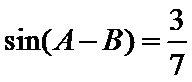
17.求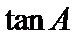
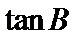
18.若AB=6,求AB边上的高CD
正确答案
(Ⅰ)证明: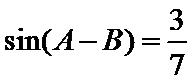
所以
解析
(Ⅰ)证明: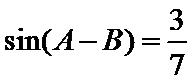
所以
考查方向
解题思路
该题解题思路如下
1)利用两角和差公式 对解析式化简
2)由已知可得到角的范围
易错点
该题对于三角形中的角的关系出错,和角公式展开化简计算错误
正确答案
(II)解: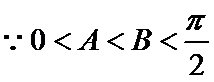
即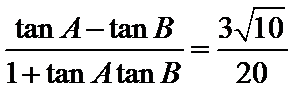
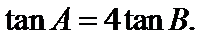
解得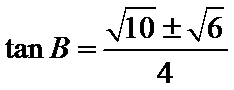
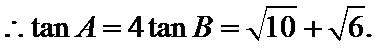
设AB边上的高为CD.
则AB=AD+DB=
或AB=AD+DB=
由AB=6,得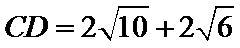
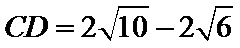
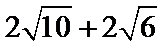
解析
(II)解: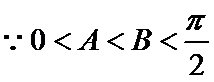
即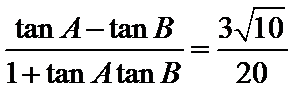
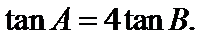
解得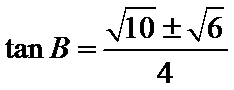
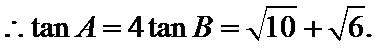
设AB边上的高为CD.
则AB=AD+DB=
或AB=AD+DB=
由AB=6,得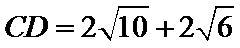
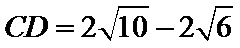
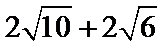
考查方向
解题思路
该题解题思路如下
对解析式解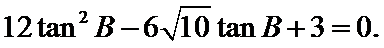
易错点
该题对于三角形中的角与边的关系出错
扫码查看完整答案与解析