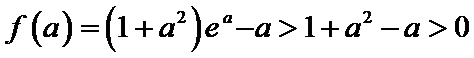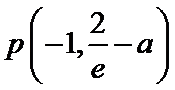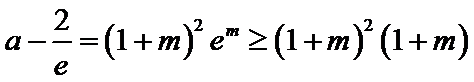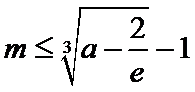- 导数与积分
- 共3028题
已知函数f(x)=
27.当a为何值时,x轴为曲线
28.用


正确答案
(Ⅰ)
解析
(Ⅰ)设曲线






因此,当


考查方向
解题思路
(Ⅰ)先利用导数的几何意义列出关于切点的方程组,解出切点坐标与对应的
易错点
本题在用切线的斜率易错
正确答案
(Ⅱ)当







解析
(Ⅱ)当


∴
当










当


(ⅰ)若









(ⅱ)若








①若



②若


③若







综上,当







考查方向
解题思路
(Ⅱ)根据对数函数的图像与性质将



易错点
本题在讨论零点的过程中易错。
设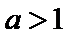
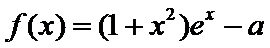
24.求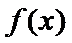
25.证明: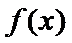
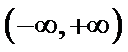
26.若曲线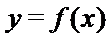
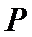
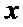
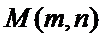
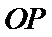
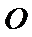
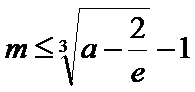
正确答案
(1)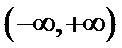
解析
(1)依题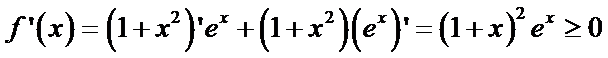
∴ 
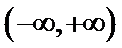
考查方向
解题思路
第一问,求导,判断导函数的正负。第二问,结合第一问的结论,再利用零点存在性定理,找到一个取正以及取负的点。第三问,先求出点P的坐标,利用平行关系找到m与a的关系,再构造函数利用单调性、最值等知识求解。
易错点
第一问是求导以及导函数正负的判断。第二问要找到函数取得正值和负值的点。第三问,导数与切线的关系以及不等式的变形。
正确答案
(2)见解析
解析

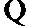
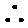
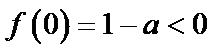
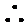
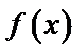
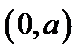
又由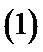
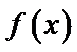
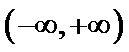

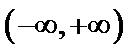
考查方向
解题思路
第一问,求导,判断导函数的正负。第二问,结合第一问的结论,再利用零点存在性定理,找到一个取正以及取负的点。第三问,先求出点P的坐标,利用平行关系找到m与a的关系,再构造函数利用单调性、最值等知识求解。
易错点
第一问是求导以及导函数正负的判断。第二问要找到函数取得正值和负值的点。第三问,导数与切线的关系以及不等式的变形。
正确答案
(3)见解析.
解析
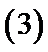

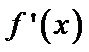
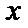
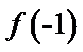
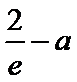
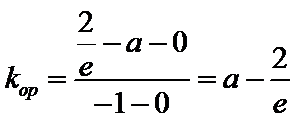
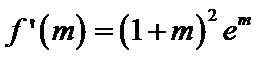
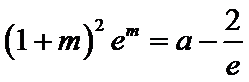
令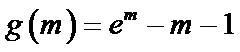
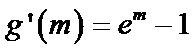

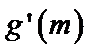
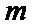
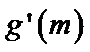

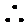
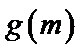

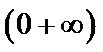
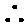
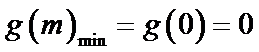
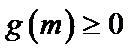
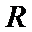
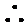
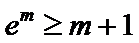
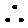
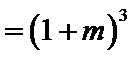
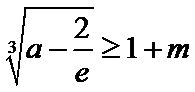
考查方向
解题思路
第一问,求导,判断导函数的正负。第二问,结合第一问的结论,再利用零点存在性定理,找到一个取正以及取负的点。第三问,先求出点P的坐标,利用平行关系找到m与a的关系,再构造函数利用单调性、最值等知识求解。
易错点
第一问是求导以及导函数正负的判断。第二问要找到函数取得正值和负值的点。第三问,导数与切线的关系以及不等式的变形。
18.设




正确答案
解析
由题意得:因为





考查方向
解题思路
当n→+∞时,直线
易错点
数列数列极限思想的正确理解运用
知识点
5.已知抛物线




正确答案
解析
设倾斜角为




考查方向
解题思路
利用焦半径公式即可得到。
易错点
点M在x轴上方和下方时候斜率的变化。
知识点
15.已知


正确答案
解析
有二项式展开的通项公式可得
所以令
所以原式=
考查方向
二项式定理;微积分基本定理
解题思路
由条件利用二项式展开式的通项公式求得a的值
再利用积分的运算性质、法则求出要求出的式子
易错点
展开式定理记忆混淆
知识点
某班同学
年龄段分组
[20,25)
[25,30)
[30,35)
[35,
[40,45)
频数
300
320
160
160
40
20
19.在答题卡上作出这些数据的频率分布直方图;
20.估计年龄段的“低头族”的平均年龄(同一组中的数据用该组区间的中点值作代表);
21.从年龄段在[25,35)的“低头族”中采用分层抽样法抽取6人接受采访,并从6人中随机选取2人作为嘉宾代表,求选取的2名嘉宾代表中恰有1人年龄在[25,30)岁的概率.
正确答案
详见解析
解析
根据频率分布表画出频率分布直方图即可
考查方向
频率分布直方图
解题思路
根据题意在分布直方图上标记
易错点
马虎大意
正确答案
详见解析
解析
设“低头族”平均年龄为
则

考查方向
平均数的计算
解题思路
根据平均数的定义即可求出
易错点
计算错误
正确答案
详见解析
解析
所有的可能情况为15种,恰有一人年龄在区间内的可能性有8种,所以概率为
考查方向
分层抽样 求等可能事件的发生的概率
解题思路
根据分层抽样的方法作出两个部分的人数,列举出所有试验发生包含的事件和满足条件的事件,根据等可能事件的概率公式,得到结果
易错点
计算能力弱,对数据敏感度不高
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
设函数

(1) 讨论
(2)当


正确答案
见解析。
解析
此题以三次函数的导数运用为背景,考察分类讨论思想运用以及分析问题和解决问题的能力。
(1)f/(x)=-3x2-2x+1+a(a>0),定义域R。f/(x)=0时,∆=4+12(1+a)>0,解得x1=
X2=
可见,




(2)由
有下列两种情况:
一是a≧4时,



二是0<a<4时,f(x)在【0,

这样,x=

又f(0)=1,f(1)=a,若a=1,则x=1或x=0时,


知识点
节日前夕,小李在家门前的树上挂了两串彩灯,这两串彩灯的第一次闪亮相互独立,且都在通电后的4秒内任一时刻等可能发生,然后每串彩灯以4秒为间隔闪亮,那么这两串彩灯同时通电后,它们第一次闪亮的时刻相差不超过2秒的概率是( )。
正确答案
解析
设两串彩灯第一次闪亮的时刻分别为x,y,则由题意可得,0≤x≤4,0≤y≤4;而所求事件“两串彩灯同时通电后,第一次闪亮相差不超过2秒”={(x,y)||x-y|≤2},由图示得,该事件概率
知识点
扫码查看完整答案与解析