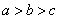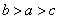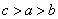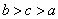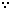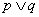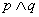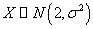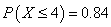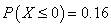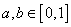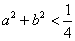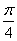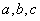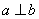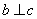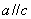- 导数与积分
- 共3028题
若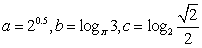
正确答案
解析
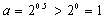
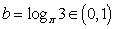
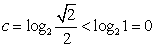
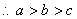
知识点
已知函数
(1)当

(2)若



正确答案
见解析。
解析
(1)
其判别式
因为


所以,

(2)当







当





因为
(或
由
①当











②当
















综上所述
知识点
下表是某市从3月份中随机抽取的10天空气质量指数(AQI)和“PM2.5”(直径小于等于2.5微米的颗粒物)24小时平均浓度的数据,空气质量指数(AQI)小于100表示空气质量优良。
(1)根据上表数据,估计该市当月某日空气质量优良的概率;
(2)在上表数据中,在表示空气质量优良的日期中,随机抽取两个对其当天的数据作进一步的分析,设事件M为“抽取的两个日期中,当天‘PM2.5’的24小时平均浓度不超过75
(3)在上表数据中,在表示空气质量优良的日期中,随机抽取3天,记


正确答案
见解析。
解析
(1)由上表数据知,10天中空气质量指数(AQI)小于100的日期有:
A2 、A3 、A5 、A9 、A10共5天,故可估计该市当月某日空气质量优良的概率
(2)由(1)知10天中表示空气质量为优良的天数为5,当天“PM2.5”的24小时平均浓度不超过75
故事件M发生的概率
(3)由(1)知,
且

故


知识点
已知函数

(1)函数



(2)若




(3)当




正确答案
见解析。
解析
(1)∵


∴函数






则
(2)当

∴
当



则
∴

(3)不妨设


∵函数



∴
∴

即
等价于
等价于
等价于
∴


知识点
下列说法正确的是
正确答案
解析
略
知识点
已知角




正确答案
解析
略
知识点
已知





正确答案
解析
略
知识点
(本题满分12分)
中国男子篮球职业联赛总决赛采用七场四胜制(即先胜四场者获胜),进入总决赛的甲乙两队中,若每一场比赛甲队获胜的概率为


(1)求甲队获得这次比赛胜利的概率;
(2)设比赛结束时两队比赛的场数为随机变量


正确答案
见解析。
解析
(1)设甲队获胜为事件


设甲队以


设甲队以



(2)随机变量





(或者


知识点
若从总体中随机抽取的样本为
正确答案
解析
略
知识点
已知函数


正确答案

解析




知识点
扫码查看完整答案与解析