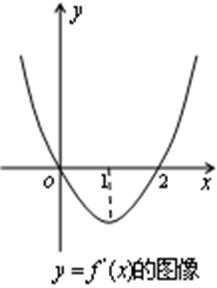
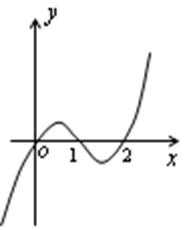
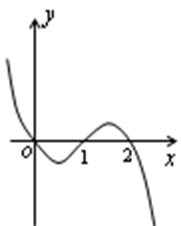
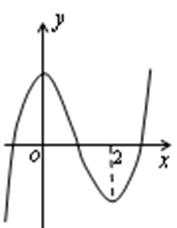- 导数与积分
- 共3028题
12.若满足




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.设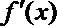

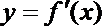
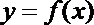
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知二次函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
23.已知函数






设函数
(1)求函数

(2)设







(3)试探究由函数


注:已知数列





正确答案
(1)


所以,函数

(2)


则


所以,数列



(3)

因为

则数列


因为
数列

故


所以
解析
解析已在路上飞奔,马上就到!
知识点
19.已知函数



(Ⅰ)当

(Ⅱ)要使函数

(Ⅲ)若对(Ⅱ)中所求的取值范围内的任意参数



正确答案
(I)当

则

(II)

由

当

因此,函数


要使


(III)解:由(II)知,函数


由题设,函数



由(II),参数
要使不等式


综上,解得



解析
解析已在路上飞奔,马上就到!
知识点
12. 已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知椭圆

正确答案
解析
因为

知识点
21.设





(1)求证:数列
(2)设数列




(3)在满足(2)的条件下,求数列


正确答案
(1)证明:当


当


又


∴ 数列

(2)解:由(1)得,

∵


∴

∴


(3)解:由(2)知

所以
即
则
②-①得
故
解析
解析已在路上飞奔,马上就到!
知识点
14.已知等差数列





正确答案
18
解析
解析已在路上飞奔,马上就到!
知识点
4.将一个四棱锥的每个顶点染上一种颜色,并使同一条棱上的两个端点异色,若只有5种颜色可供使用,则不同的染色方法总数有( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析