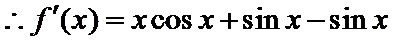- 导数与积分
- 共3028题
10.已知函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知函数f(x)=|sin x|的图象与直线y=kx(k>0)有且仅有三个交点,交点的横坐标的最大值为α,令m=

正确答案
解析
作出函数f(x)=|sin x|的图象与直线y=kx(k>0)的图象,如图.
要是两个函数有且仅有三个交点,则由图象可知,直线在(π,
当x∈(π,
此时f'(x)=-cos x,则-cos α=-
所以m=



知识点
13.已知函数
正确答案
4
解析
∵ 
∴
知识点
7.设曲线


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知

(1)讨论函数
(2)若函数

①求实数
②求证:
正确答案
见解析
解析
(1)


①当


②当




所以


(2)①由(I)知,当


当







所以

此时,

令

所以


所以
②证法一:
下面证明:当

设





即当






②证法二:
令
则:
所以函数



于是
又

考查方向
解题思路
1利用导数求函数单调性,2根据函数的零点求参数的取值范围
3构造函数求两个零点和的范围
易错点
本题必须注意函数的定义域,以及对参数进行讨论,否则求解错误。
知识点
21.己知函数f(x)=a(x-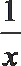
(1)若f(x)有极值,求a的取值范围;
(2)讨论(x)的零点个数,并说明理由.(参考数值:ln2≈0. 6931)
正确答案
(1)0<a<1;
(2)当a≤0或a≥1时,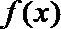
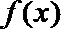
解析
本题属于导数应用中的基本问题,题目的难度是逐渐由易到难,
(1)直接按照步骤来求;
(2)要注意对参数的讨论.
(1)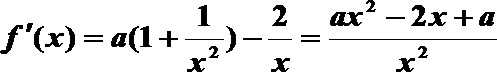
因为f(x)定义域为(0,+∞),
所以ax2-2x+a=0有正根且不为等根。
显然a≠0,由x1x2=1>0.得Δ>0且x1+x2>0,所以 0<a<1 。
(2)由上知,
因为x∈(0,+∞),①若a≤0,则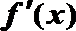
②若a≥1,则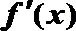
③若0<a<1,记x1,x2分别为ax2-2x+a=0的两根,且x1<1<x2,且f(x)在(0,x1)单调递增,在(x1,x2)单调递增,(x2,+∞)单调递增。
因为f(1)=0,所以f(x1)>0,f(x2)<0.当x∈(0,x1)时,取
显然,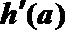
所以h(a)在(0,1)单调递增,所以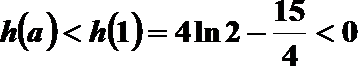
故
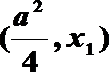
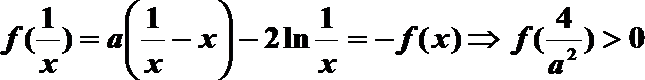
则f(x)在
综上可知:当a≤0或a≥1时,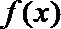
考查方向
本题考查了利用导数求含参数的函数极值,分类讨论,讨论点大体可以分成以下几类:
1、根据判别式讨论;
2、根据二次函数的根的大小;
3、定义域由限制时,根据定义域的隐含条件;
4、求导形式复杂时取部分特别常常只需要转化为一个二次函数来讨论;
5、多次求导求解等.
解题思路
无
易错点
第二问中的易丢对a的分类讨论。
知识点
12.已知定义在R上的奇函数







正确答案
解析
由












考查方向
解题思路
根据题目中的信息画出符合条件的函数的草图,结合草图利用函数的周期性予以解决。
易错点
本题容易因为不理解
知识点
12.函数

正确答案
解析
首先构造两个函数


(1)当

(2)当

(3)当



考查方向
解题思路
首先构造两个函数


易错点
1、忽略对数函数的定义域导致结果出错
2、没有注意到后面的二次函数过原点,而增加不必要的讨论和计算
知识点
21. 已知函数
(Ⅰ)设函数

(Ⅱ)若不等式


正确答案
见解析
解析
(Ⅱ)
①当


令




②当



综上,当



当

(Ⅱ)由题意可知,不等式

即在[1,e]存在

由(Ⅰ)中

即函数
由(Ⅰ)知,当

当
①当


②当



③当






综上可得,实数

考查方向
解题思路
确定函数的定义域,利用导数求函数的单调区间,根据题意构造出恰当的不等式,进而求出参数的取值范围。
易错点
求导错误,构造函数不成功。
知识点
8. 设函数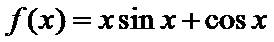
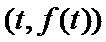
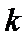
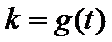
正确答案
解析
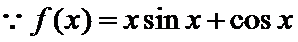
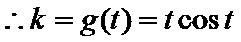
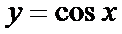
考查方向
解题思路
先求导数,然后利用导函数求k的解析式,进而判断函数图象
易错点
求导错误,函数单调性不会判断
知识点
扫码查看完整答案与解析