- 导数与积分
- 共3028题
已知函数
23.求函数
24.当


25.试问过点

正确答案
(1)当






解析
试题分析:本题属于导数应用中的基本问题,题目的难度是逐渐由易到难,(1)利用导函数对
(Ⅰ)函数


(1)当



考查方向
解题思路
本题考查导数的性质及其应用,解题步骤如下:
求出原函数的导函数,对






易错点
第一问在对
第三问在利用导数研究 “过点问题”的切线方程求法上易出错。
正确答案







解析
试题分析:本题属于导数应用中的基本问题,题目的难度是逐渐由易到难,(1)利用导函数对
(Ⅱ)由(Ⅰ)可知,
(1)当



所以在区间



(2)当



上为增函数,所以
依题意有


(3)当



所以
依题意有


综上所述,当


考查方向
解题思路
本题考查导数的性质及其应用,解题步骤如下:
求出原函数的导函数,对






易错点
第一问在对
第三问在利用导数研究 “过点问题”的切线方程求法上易出错。
正确答案
当



解析
试题分析:本题属于导数应用中的基本问题,题目的难度是逐渐由易到难,(1)利用导函数对
(Ⅲ)设切点为

切线方程为
因为切线过点


令


(1)当



在区间


所以函数

故方程

因此当

(2)当



在区间





取

故

取

设


当

所以



故

因此当

(3)当


综上所述,当

当

考查方向
解题思路
本题考查导数的性质及其应用,解题步骤如下:
求出原函数的导函数,对






易错点
第一问在对
第三问在利用导数研究 “过点问题”的切线方程求法上易出错。
已知函数



25.求函数
26.求证:
正确答案
(Ⅰ)

解析
解:(1)
令



令



考查方向
解题思路
在(Ⅱ)中要构造函数,通过求导研究单调性.
易错点
求单调性注意定义域;导数的运算.
正确答案
(Ⅱ)略.
解析


则
令
则


而



即

则





则


故

故
考查方向
解题思路
在(Ⅱ)中要构造函数,通过求导研究单调性.
易错点
求单调性注意定义域;导数的运算.
已知函数




25.若函数

26.当(Ⅰ)中的

正确答案
解析
(1)解:
①



而

故

②





令



若

若


又
令

令



令



故


则
故


综上,

考查方向
解题思路
利用导数讨论函数的单调性与极值,并与图像结合。
利用第一问的结论化简左边的函数式,然后讨论函数的单调性和极值,即可得到结果。
易错点
忽视了函数的定义域
第一问中没有对k进行分类讨论
第二问的证明过程中不能正确利用第一问的结论化简函数。
正确答案
证明略
解析
由(1)知,


而

则

记

令



而



即
则





则


故

故
考查方向
解题思路
利用导数讨论函数的单调性与极值,并与图像结合。
利用第一问的结论化简左边的函数式,然后讨论函数的单调性和极值,即可得到结果。
易错点
忽视了函数的定义域
第一问中没有对k进行分类讨论
第二问的证明过程中不能正确利用第一问的结论化简函数。
设函数


正确答案
解析
由







考查方向
解题思路
由






易错点
本题易在数列求和运算上出错。
知识点
4.下列三个数:
正确答案
知识点
根据破产法律制度的规定,下列各项中,属于破产财产的有( )。
A.宣告破产时破产企业经营管理的全部财产
B.破产企业的对外投资及应得收益
C.破产企业享有的专利权
D.企业破产前,为维持生产经营向职工筹借的款项
正确答案
A,B,C
解析
[解析] 根据《破产法》规定,企业在破产前为维持生产经营,向职工筹借的款项,视为破产企业所欠职工工资处理,借款利息按照借款实际使用时间和银行同期存款利率计算,但职工在企业破产前作为资本金投资的款项,应当作为破产财产。
17.某山区外围有两条相互垂直的直线型公路,为进一步改善山区的交通现状,计划修建一条连接两条公路和山区边界的直线型公路,记两条相互垂直的公路为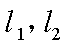
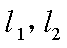
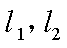
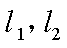
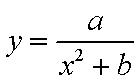
(1)求a,b的值;
(2)设公路l与曲线C相切于P点,P的横坐标为t.
①请写出公路l长度的函数解析式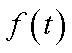
②当t为何值时,公路l的长度最短?求出最短长度.
正确答案
(1)由题意知,点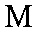
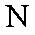
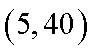
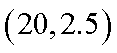
将其分别代入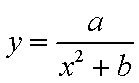
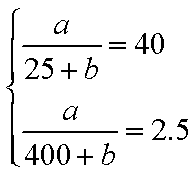
解得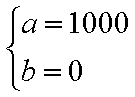
(2)①由(1)知,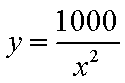

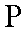
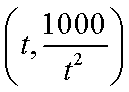
设在点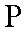
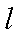
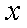
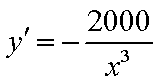
则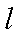
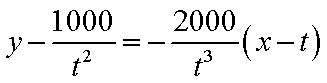
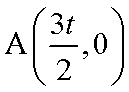
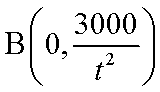
故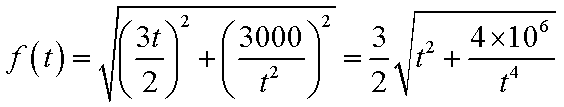
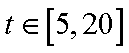
②设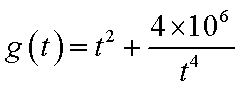
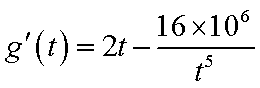
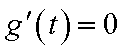
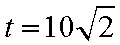
当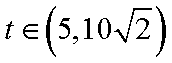
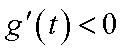
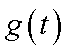
当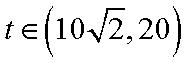
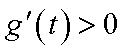
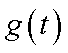
从而,当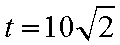
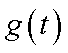
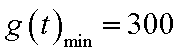
此时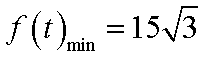
答:当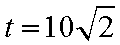
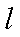
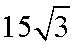
解析
解析已在路上飞奔,马上就到!
知识点
12.设函数






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知函数
(1)试讨论
(2)若


正确答案
(1)



当




当




所以函数



当




所以函数



(2)由(1)知,函数



零点等价于


又




设







从而


此时,
因函数有三个零点,则

所以

解得
综上
解析
解析已在路上飞奔,马上就到!
知识点
21.(本题满分12分)
设函数
(Ⅰ)证明:


(Ⅱ)若对于任意


正确答案
(Ⅰ)详见解析;(Ⅱ)
试题分析:(Ⅰ)先求导函数



(Ⅱ)








解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析