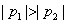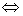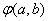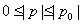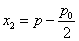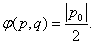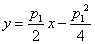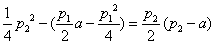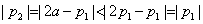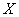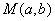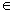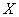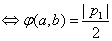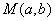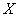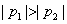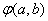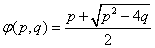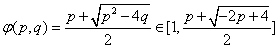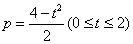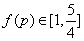导数与积分
共3028题

导数与积分
共3028题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 20 分

请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。

正确答案

测试

题型：填空题

填空题 · 20 分

请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。

正确答案

测试

题型：简答题

简答题 · 10 分

盒中共有9个球，其中有4个红球，3个黄球和2个绿球，这些球除颜色外完全相同。

（1）从盒中一次随机取出2个球，求取出的2个球颜色相同的概率P；

（2）从盒中一次随机取出4个球，其中红球、黄球、绿球的个数分别记为，随机变量X表示中的最大数，求X的概率分布和数学期望。

正确答案

见解析。

解析

（1）一次取2个球共有种可能情况，2个球颜色相同共有种可能情况

∴取出的2个球颜色相同的概率

（2）X的所有可能取值为，则

∴X的概率分布列为

故X的数学期望

知识点

导数的加法与减法法则

题型：简答题

简答题 · 14 分

在平面直角坐标系上,给定抛物线:,实数满足,是方程的两根，记.

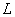
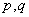
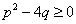
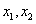
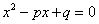
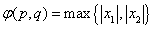
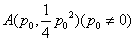
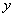
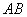
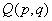
（1）过点作的切线交轴于点.证明:对线段上任一点有

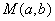
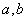
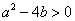
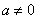
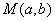
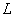
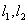
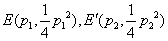
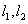
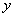
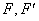
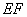
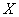
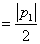
（2）设是定点，其中满足,.过作的两条切线，切点分别为，与轴分别交与.线段上异于两端点的点集记为.证明:;

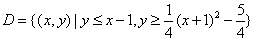
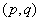
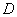
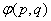
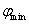
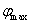
（3）设.当点取遍时，求的最小值(记为)和最大值(记为)。

正确答案

见解析

解析

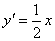
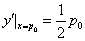
（1）因为,所以,过点的切线方程为

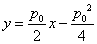
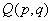
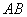
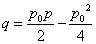
即,从而,又在直线上,故,其中

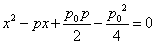
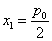
所以方程为,解得,

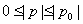
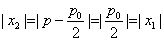
由于,且同号,所以,所以

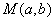
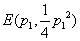
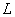
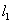
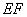
（2）过点且切点为的的切线方程为:

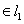
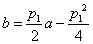
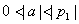
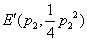
因为,所以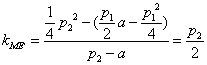且,因为,

所以,即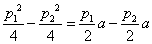

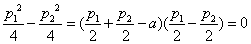
即,所以,所以

因为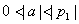,且同号,所以

反之也成立,所以,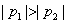

由（1）可知,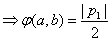,反之,逆推也成立,所以

综上,.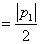

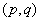
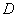
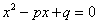
（3）此题即求当点取遍时,方程的绝对值较大的根的最大值与最小值,

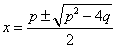
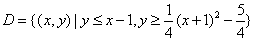
解方程得,因为,

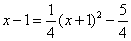
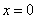
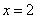
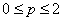
令,解得或，所以，

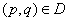
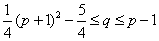
因为，所以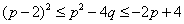，于是

所以，所以

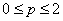
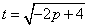
设（），令，则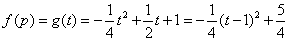

则，所以

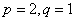
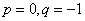
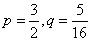
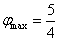
综上，当或时，；当时，.

知识点

导数的加法与减法法则

题型：单选题

单选题 · 5 分

现安排甲、乙、丙、丁、戌5名同学参加上海世博会志愿者服务活动，每人从事翻译、导游、礼仪、司机四项工作之一，每项工作至少有一人参加。甲、乙不会开车但能从事其他三项工作，丙丁戌都能胜任四项工作，则不同安排方案的种数是

A152

B126

C90

D54

正确答案

解析

分类讨论：若有2人从事司机工作，则方案有；若有1人从事司机工作，则方案有种，所以共有18+108=126种，故B正确

知识点

导数的加法与减法法则

题型：填空题

填空题 · 5 分

已知，式中变量，满足约束条件，则的最大值为___________.

正确答案

解析

依题意，画出可行域（如图示），

则对于目标函数y=2x-z，

当直线经过A（2，－1）时，

z取到最大值，.

知识点

导数的加法与减法法则

题型：填空题

填空题 · 5 分

圆柱形容器内部盛有高度为8cm的水，若放入三个相同的球（球的半径与圆柱的底面半径相同）后，水恰好淹没最上面的球（如图所示），则球的半径是 cm。

正确答案

解析

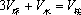
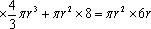
设球半径为r，则由可得,解得r=4.

知识点

导数的加法与减法法则

题型：填空题

填空题 · 5 分

已知函数，若对任意，都有成立，则实数m的取值范围是。

正确答案

解析

略

知识点

导数的加法与减法法则

题型：简答题

简答题 · 10 分

如图，AB是圆O的直径，C、 D是圆O 上位于AB异侧的两点

证明:∠OCB=∠D.

正确答案

见解析。

解析

因为B, C是圆O上的两点，所以OB=OC.

故∠OCB=∠B.

又因为C, D是圆O上位于AB异侧的两点，

故∠B，∠D为同弧所对的两个圆周角，

所以∠B=∠D.

因此∠OCB=∠D.

知识点

导数的加法与减法法则

题型：填空题

填空题 · 5 分

如图所示，程序框图（算法流程图）的输出结果是 .

正确答案

解析

略

知识点

导数的加法与减法法则

继续学习棒棒哒，已是最后一个知识点

已完结

百度题库 > 高考 > 理科数学 > 导数与积分

扫码查看完整答案与解析