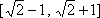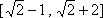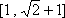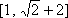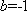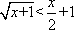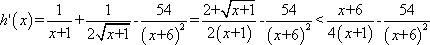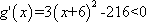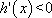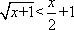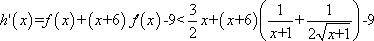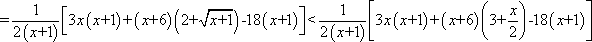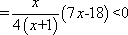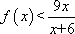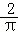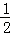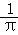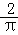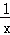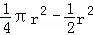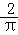- 导数与积分
- 共3028题
已知
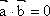

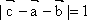
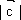
正确答案
解析
略
知识点
如图,圆锥顶点为P,底面圆心为O,其母线与底面所成的角为22.5°,AB和CD是底面圆O上的两条平行的弦,轴OP与平面PCD所成的角为60°。
(1)证明:平面PAB与平面PCD的交线平行于底面;
(2)求cos∠COD.
正确答案
见解析
解析
(1)证明:设面PAB与面PCD的交线为l.
因为AB∥CD,AB不在面PCD内,
所以AB∥面PCD.
又因为AB
由直线AB在底面上而l在底面外可知,l与底面平行。
(2)解:
由圆的性质,∠COD=2∠COF,OF⊥CD.
因为OP⊥底面,CD
所以OP⊥CD.
又OP∩OF=O,故CD⊥面OPF.
又CD
从而直线OP在面PCD上的射影为直线PF,
故∠OPF为OP与面PCD所成的角。
由题设,∠OPF=60°。设OP=h,
则OF=OP·tan∠OPF=h·tan 60°=
根据题设有∠OCP=22.5°,
得
由1=tan 45°=
可解得tan 22.5°=-1,
因此
在Rt△OCF中,cos∠COF=
故cos∠COD=cos(2∠COF)=2cos2∠COF-1=
知识点
设全集为R,函数f(x)=

正确答案
解析
要使函数f(x)=

知识点
已知动圆过定点A(4,0),且在y轴上截得弦MN的长为8.
(1)求动圆圆心的轨迹C的方程;
(2)已知点B(-1,0),设不垂直于x轴的直线l与轨迹C交于不同的两点P,Q,若x轴是∠PBQ的角平分线,证明直线l过定点。
正确答案
(1)y2=8x.;(2) (1,0)
解析
(1)
如图,设动圆圆心O1(x,y),由题意,|O1A|=|O1M|,
当O1不在y轴上时,
过O1作O1H⊥MN交MN于H,则H是MN的中点,
∴

∴
化简得y2=8x(x≠0)。
又当O1在y轴上时,O1与O重合,点O1的坐标(0,0)也满足方程y2=8x,
∴动圆圆心的轨迹C的方程为y2=8x.
(2)
证明:由题意,设直线l的方程为y=kx+b(k≠0),P(x1,y1),Q(x2,y2),
将y=kx+b代入y2=8x中,
得k2x2+(2bk-8)x+b2=0,
其中Δ=-32kb+64>0.
由求根公式得,x1+x2=
x1x2=
因为x轴是∠PBQ的角平分线,
所以
即y1(x2+1)+y2(x1+1)=0,
(kx1+b)(x2+1)+(kx2+b)(x1+1)=0,
2kx1x2+(b+k)(x1+x2)+2b=0,③
将①,②代入③得2kb2+(k+b)(8-2bk)+2k2b=0,
∴k=-b,此时Δ>0,
∴直线l的方程为y=k(x-1),
即直线l过定点(1,0)
知识点
在直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴建立极坐标系,已知射线θ=

正确答案
(2.5,2.5)
解析
射线θ=

联立方程并消元可得x2﹣5x+4=0,∴方程的两个根分别为1,4
∴线段AB的中点的横坐标为2.5,纵坐标为2.5
∴线段AB的中点的直角坐标为(2.5,2.5)。
知识点
设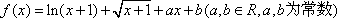
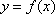
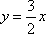
(1)求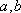
(2)证明:当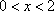
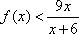
正确答案
见解析
解析
(1)由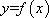
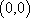
由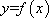
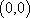

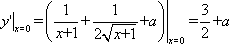
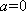
(2)(证法一)由均值不等式,当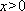
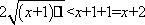
记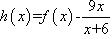

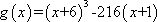
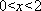
因此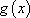
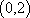
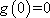
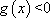
因此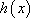
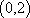
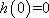

于是当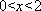
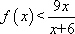
(证法二)
由(1)知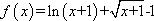
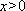

令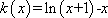
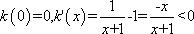
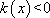
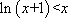
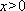
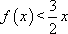
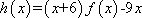
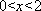
因此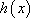
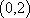
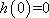
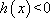
知识点
某学校有男、女学生各500名.为了解男女学生在学习兴趣与业余爱好方面是否存在显著差异,拟从全体学生中抽取100名学生进行调查,则宜采用的抽样方法是
正确答案
解析
略
知识点
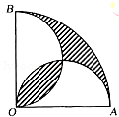
如图,在圆心角为直角的扇形OAB中,分别以OA,OB为直径作两个半圆,在扇形OAB内随机取一点,则此点取自阴影部分的概率是( )
正确答案
解析
设OA的中点是D,则∠CDO=90°,半径为r
S扇形OAB=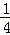
S半圆OAC=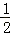
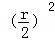
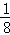
S△ODC=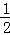
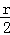
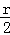
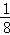
S弧OC=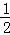
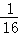
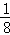
两个圆的弧OC围成的阴影部分的面积为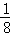
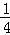
图中阴影部分的面积为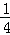
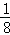
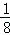
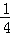
∴此点取自阴影部分的概率是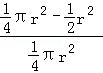
故选A。
知识点
已知



正确答案
解析
略
知识点
已知函数

(1)求
(2)若

正确答案
(1)


(2)
解析
(1)
令
得:


得:
且单调递增区间为
(2)
①当





②当
得:当
令
当
当

知识点
扫码查看完整答案与解析