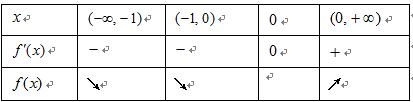- 导数与积分
- 共3028题
3.设a>0 a≠1 ,则“函数f(x)= ax在R上是减函数 ”,是“函数g(x)=(2-a) 
正确答案
解析
p:“函数f(x)= ax在R上是减函数 ”等价于



知识点
现有16张不同的卡片,其中红色、黄色、蓝色、绿色卡片各4张,从中任取3张,要求这些卡片不能是同一种颜色,且红色卡片至多1张,不同取法的种数为
正确答案
解析
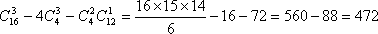
另解: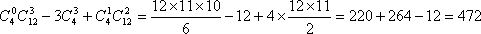
知识点
设



正确答案
解析
略。
知识点
如果函数



正确答案
解析
略。
知识点
已知点P是△ABC的中位线EF上任意一点,且EF//BC,实数x,y满足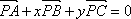
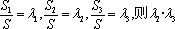
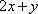
正确答案
解析
略。
知识点
已知函数



(1)求
(2)当


(3)证明:当



正确答案
见解析。
解析
(1)解:∵

∵直线


∴


(2)解法1:由(1)得
当



令

令

当




从而,当



故
因此,当


∴所求

解法2:由(1)得
当


令

方程

(ⅰ)当




故函数

由于
则当


(ⅱ)当



故函数


(ⅲ) 当


则



故函数


从而,函数


而
由(ⅱ)知,当

得

故当

综上所述,

(3)证明:由(2)得,当


又
从而,
把

知识点
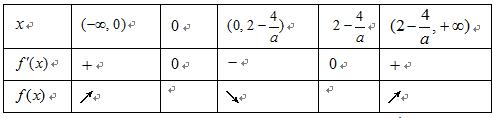
已知函数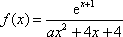
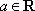
(1)若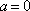
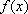
(2)当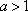
正确答案
见解析
解析
(1)解:函数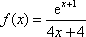
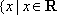
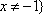
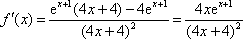
令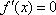
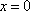
当
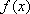
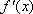
……………… 5分
故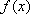
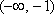
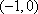
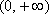
所以当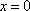
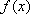
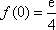
(2)解:因为 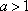
所以 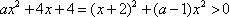
所以函数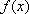
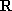
求导,得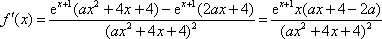
令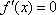
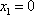

当 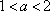
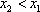
当
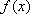
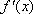
故函数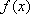
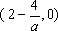
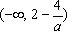
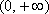
……………… 11分
当 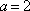
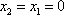
因为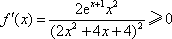
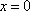
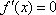
所以函数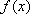
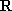
当 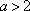
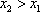
当
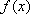
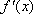
故函数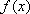
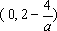
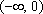

综上,当 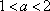
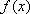
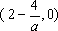
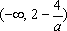
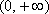
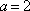
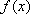
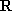
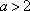
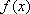
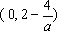
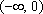
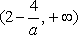
知识点
在




正确答案
解析
略。
知识点
等差数列{an}中,a4+ a10+ a16=30,则a18-2a14的值为 。
正确答案
-10
解析
略。
知识点


正确答案
一或三
解析
略
知识点
扫码查看完整答案与解析