- 导数与积分
- 共3028题
已知集合




(1)求证:
(2)求证:
(3)对于

正确答案
见解析。
解析
(1)证明:依题意有

因此
可得
所以
即
(2)证明:由(1)可得
又


同理

又

所以
当


可知
又当

所以
(3)解:对于任意

由


因此,只需对

因为



因此可设




由


由


由


由


所以满足条件的一个集合
知识点
已知函数f(x)=lnx,g(x)=f(x)+ax2+bx,函数g(x)的图象在点(1,g(1))处的切线平行于x轴。
(1)确定a与b的关系;
(2)试讨论函数g(x)的单调性;
(3)证明:对任意n∈N*,都有ln(1+n)>
正确答案
见解析。
解析
(1)依题意得g(x)=lnx+ax2+bx,
则
由函数g(x)的图象在点(1,g(1))处的切线平行于x轴得:g'(1)=1+2a+b=0,∴b=﹣2a﹣1。
(2)由(1)得

∵函数g(x)的定义域为(0,+∞),
∴①当a≤0时,2ax﹣1<0在(0,+∞)上恒成立,
由g'(x)>0得0<x<1,由g'(x)<0得x>1,
即函数g(x)在(0,1)上单调递增,在(1,+∞)单调递减;
②当a>0时,令g'(x)=0得x=1或
若



即函数g(x)在

若



即函数g(x)在(0,1),

若

即函数g(x)在(0,+∞)上单调递增,
综上得:当a≤0时,函数g(x)在(0,1)上单调递增,在(1,+∞)单调递减;
当


当
当


(3)证法一:由(2)知当a=1时,函数g(x)=lnx+x2﹣3x在(1,+∞)单调递增,∴lnx+x2﹣3x≥g(1)=﹣2,即lnx≥﹣x2+3x﹣2=﹣(x﹣1)(x﹣2),
令

∴



∴
即
证法二:构造数列{an},使其前n项和Tn=ln(1+n),
则当n≥2时,
显然a1=ln2也满足该式,
故只需证
令
则
∴
以下同证法一。
证法三:令φ(n)=ln(1+n)﹣
则

令

∵
又h(1)=0,∴当x∈(1,2]时,h(x)>0,即φ(n+1)﹣φ(n)>0,
∴数列φ(n)单调递增,又φ(1)=ln2>0,∴即
知识点
设a,b为大于1的正数,并且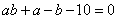
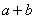
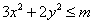
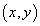
正确答案
解析
略
知识点
双曲线








正确答案
解析
略
知识点
已知椭圆

(1)求椭圆C1的方程;
(2)设椭圆C1的左焦点为F1,右焦点为F2,直线l1过点F1且垂直于椭圆的长轴,动直线l2垂直于直线l1,垂足为点P,线段PF2的垂直平分线交l2于点M,求点M的轨迹C2的方程;
(3)设C2与x轴交于点Q,不同的两点R,S在C2上,且满足

正确答案
见解析。
解析
(1)由
得


(2)由MP=MF2得动点M的轨迹是以l1:x=﹣1为准线,
F2为焦点的抛物线,∴点M的轨迹C2的方程为y2=4x,
(3)Q(0,0),设
∴
由

∴化简得
∴
∵
又∵y22≥64,∴当y22=64,即y2=±8时
∴

知识点
已知x、y使方程x2+y2-2x -4y + 4 = 0,则
正确答案
解析
略
知识点
若




正确答案
解析
略
知识点
某商场销售甲、乙、丙三种不同型号的钢笔,甲、乙、丙三种型号钢笔数量之比依次为 2:3:4.现用分层抽样的方法抽出一个容量为n的样本,其中甲型钢笔有12支,则此样本容量n= 。
正确答案
54
解析
由n•
故答案为 54。
知识点
已知椭圆


短轴长为
(1)求椭圆的方程;
(2)过左焦点





正确答案
见解析
解析
(1)由题意,
解得
即:椭圆方程为
(2)当直线


此时
当直线



代入消去

设

所以 
原点到直线的

所以三角形的面积
由
所以直线

知识点
已知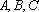
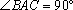

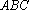
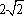
正确答案
解析
略
知识点
扫码查看完整答案与解析