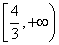- 导数与积分
- 共3028题
正确答案
见解析。
解析
(1)解:由题意
当


此时函数在


当


此时函数在


(2)取

故
取

(3)假设存在这样的切线,设其中一个切点
∴切线方程:



设






故
又
注意到


方程①有且仅有一解,故符合条件的切线有且仅有一条,…………14分
知识点
设



(1)求
(2)若


(3)求证:
正确答案
见解析。
解析
(1)
由题设


(2)


设


①若


②若

当





当






综上所述,
(3)由(2)知,当


不妨令
所以


累加可得

知识点
设f(n)是定义在N*上的增函数,f(4)=5,且满足:
①任意n∈N*,f(n)Z;②任意m,n∈N*,有f(m)f(n)=f(mn)+f(m+n-1)。
(1)求f(1),f(2),f(3)的值;
(2)求f(n)的表达式。
正确答案
见解析。
解析
(1)因为f(1)f(4)=f(4)+f(4),所以5 f(1)=10,则f(1)=2。
因为f(n)是单调增函数,
所以2=f(1)<f(2)<f(3)<f(4)=5。
因为f(n)∈Z,所以f(2)=3,f(3)=4.
(2)解:由(1)可猜想f (n)=n+1。
证明:因为f (n)单调递增,所以f (n+1)>f (n),又f(n)∈Z,
所以f (n+1)≥f (n)+1。
首先证明:f (n)≥n+1。
因为f (1)=2,所以n=1时,命题成立。
假设n=k(k≥1)时命题成立,即f(k)≥k+1。
则f(k+1)≥f (k)+1≥k+2,即n=k+1时,命题也成立。
综上,f (n)≥n+1.
由已知可得f (2)f (n)=f (2n)+f (n+1),而f(2)=3,f (2n)≥2n+1,
所以3 f (n)≥f (n+1)+2n+1,即f(n+1)≤3 f (n)-2n-1。
下面证明:f (n)=n+1。
因为f (1)=2,所以n=1时,命题成立。
假设n=k(k≥1)时命题成立,即f(k)=k+1,
则f(k+1)≤3f (k)-2k-1=3(k+1)-2k-1=k+2,
又f(k+1)≥k+2,所以f(k+1)=k+2。
即n=k+1时,命题也成立。
所以f (n)=n+1
解法二:由f(1)=2,f(2)=3,f(3)=4,f(4)=5,猜想f(n)=n+1.
下面用数学归纳法证明:
①当n=1,2,3,4时,命题成立。
②假设当n≤k (k≥4)时,命题成立,下面讨论n=k+1的情形。
若k为奇数,则k+1为偶数,且
根据归纳假设知

因为
所以
若k为偶数,则k+2,k+4为偶数,且
根据归纳假设知

因为
所以
又k+1=f(k)<f(k+1)<f(k+2)=k+3。
所以f(k+1)=k+2
因此不论k的奇偶性如何,总有f(k+1)=k+2,即n=k+1时,命题也成立
于是对一切n∈N*,f(n)=n+1,
解法三:因为f (n)单调递增,所以f (n+1)>f (n),又f(n)∈Z,
所以f (n+1)≥f (n)+1,又f(1)=2,所以f (n)≥n+1
由已知可得:f (2)f (n)=f (2n)+f (n+1)
而f(2)=3,f (2n)≥2n+1
所以3 f (n)≥f (n+1)+2n+1,即:f(n+1)≤3 f (n)-2n-1
或者f(n+1)-n-2≤3(f (n)-n-1)
所以有f(n+1)-n-2≤3(f (n)-n-1)
≤32(f (n-1)-n)
≤33(f (n-2)-n+1)
……
≤3n(f (1)-2)=0
于是f(n+1)≤n+2 又f (n+1)≥n+2
所以f(n+1)=n+2,又f(1)=2
所以f(n)=n+1
知识点
若实数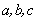
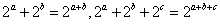
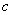
正确答案
解析
略
知识点
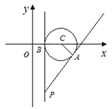
曲线Cl,C2的参数方程分别为

若点M (xo,1)在曲线Cl上,则x0____;若曲线Cl,C2有两个不同的公共点,则实数r的取值范围是____。
正确答案
0;
解析
略
知识点
已知函数
(1)若


(2)若


①求

② 求函数
正确答案
见解析
解析
(1)
∵
∴

∴
(2)∵

∵

又
∴
∴
①由



∵
∴

②
令
当



当
此时


当
此时













知识点
某高校在2011年自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100]得到的频率分布直方图如图所示。
(1)分别求第3,4,5组的频率;
(2)若该校决定在笔试成绩高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试,
(ⅰ)已知学生甲和学生乙的成绩均在第三组,求学生甲和学生乙同时进入第二轮面试的概率;
(ⅱ)学校决定在这6名学生中随机抽取2名学生接受考官D的面试,设第4组中有X名学生被考官D面试,求X的分布列和数学期望。
正确答案
见解析。
解析
解析:(1)第三组的频率为0.06×5=0.3;
第四组的频率为0.04×5=0.2;第五组的频率为0.02×5=0.1.…………3分
(2)(ⅰ)设M:学生甲和学生乙同时进入第二轮面试
(ⅱ)

知识点
已知函数
(1)当

(2)求实数


正确答案
(1)
解析
略
知识点
如果实数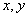
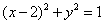
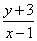
正确答案
解析
用数形结合,设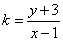
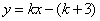
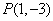
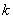
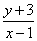
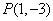
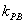
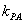
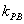
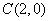
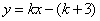
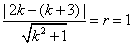
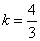
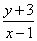
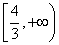
知识点
已知x,yR,且
正确答案
见解析。
解析
证: 因为|x+5y|=|3(x+y)-2(x-y)|,
由绝对值不等式性质,得
|x+5y|=|3(x+y)-2(x-y)|≤|3(x+y)|+|2(x-y)

即|x+5y|≤1.
知识点
扫码查看完整答案与解析