- 导数与积分
- 共3028题
已知点


(1)若








(2)若四边形










正确答案
见解析。
解析
(1)由点





设


(2)另设
知识点
某几何体的三视图如图示,则此几何体的体积是
正确答案
解析
此几何体为半个圆锥与半个圆柱的组合体,体积
知识点
已知椭圆



(1)求椭圆的方程;
(2)若





(3)在(2)的条件下,试问





正确答案
见解析
解析
(1)



(2)


直线


代入椭圆





(3)设存在



则由




知识点
在平面直角坐标系xOy中,已知抛物线C: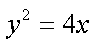
为抛物线C上异于顶点的动点,直线MF交抛物线C于另一点N,链接ME,NE并延长分别交
抛物线C与点P,Q。
(1)当MN 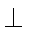
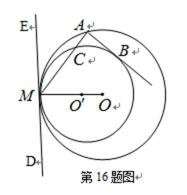
(2)当直线MN,PQ的斜率存在且分别记为k1,k2时,求证: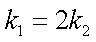
正确答案
见解析。
解析
(1)抛物线C: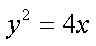
当MN 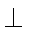
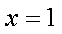
将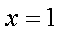
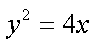
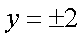
不妨设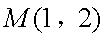
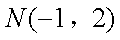
则直线ME的方程为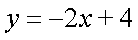
由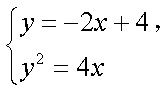
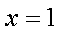
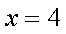
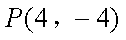
同理得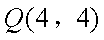
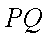
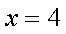
故直线PQ与x轴的交点坐标(4,0),
(2)设直线MN的方程为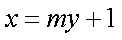
并设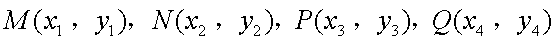
由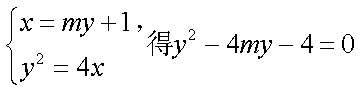
于是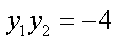
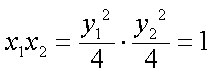
设直线MP的方程为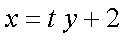
由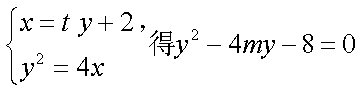
所以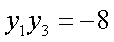
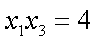
同理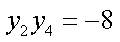
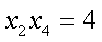
由①②③④⑤⑥,得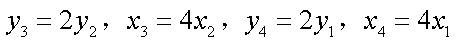
即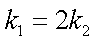
知识点
设






(1)证明:当


(2)记

正确答案
见解析。
解析
(1)当


∵


∴
=
∴当

同理可证,当

(2)由
=
=
=
又由



知识点
如图,过半径为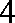
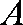
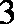
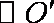
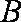
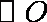

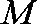
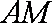
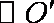

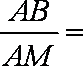
正确答案
解析
作两圆的公切线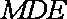
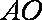
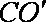
所以
由弦切角定理知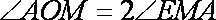
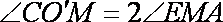
则
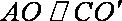
所以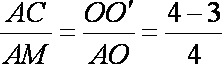

知识点
和平面解析几何的观点相同,在空间中,空间曲面可以看作是适合某种条件的动点的轨迹,在空间直角坐标系

设





(1)试建立一个适当的空间直角坐标系

(2)指出和证明曲面

正确答案
见解析
解析
解析:(1)如图,以两个定点










设


两边平方,得

两边平方,整理得
令

若点


(2)对称性:
由于点




由于点







由于点







图略, (4分)
知识点
已知函数
(1)求函数
(2)若函数
(3)若

正确答案
见解析。
解析
由已知函数


(1)函数
当




所以函数


(2)因f(x)在


所以当

又
故当


所以


(3)命题“若

“当

由(2),当


问题等价于:“当





则






故


(i)若





于是,

(ii)若





当





所以,


所以,

综上,得
知识点
已知抛物线


正确答案
解析
抛物线的焦点为











知识点
如图,MN为两圆的公共弦,一条直线与两圆及公共弦依次交于A,B,C,D,E,求证:AB•CD=BC•DE。
正确答案
见解析。
解析
∴A,M,D,N四点共圆,
所以AC•CD=MC•CN
∵M,B,N,E四点共圆,
∴BC•CE=MC•CN,
∴AC•CD=BC•CE,
即(AB+BC)•CD=BC•(CD+DE),
∴AB•CD=BC•DE。
知识点
扫码查看完整答案与解析