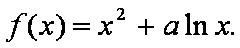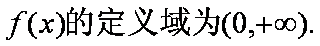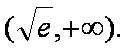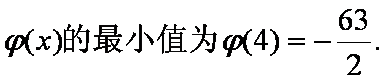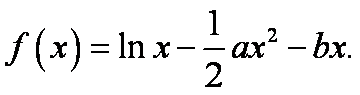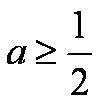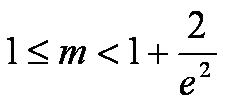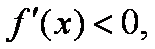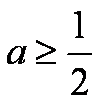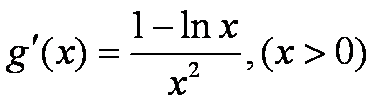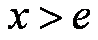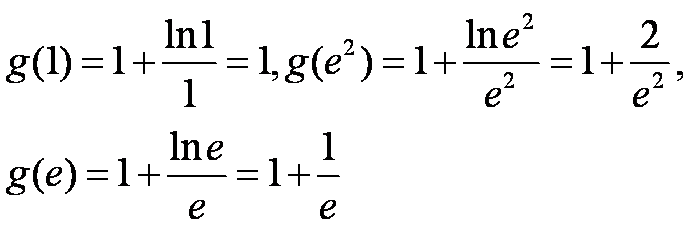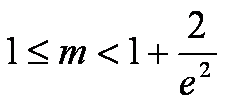- 导数与积分
- 共3028题
盒中装有形状,大小完全相同的5个球,其中红色球3个,黄色球2个,若从中随机取出2个球,已知其中一个为红色,则另一个为黄色的概率为
正确答案
解析
记红色球分别为a、b、c,黄色球分别为d、e,因为随机取出2个球,其中一个为红色,所以所有的基本事件为(a,b),(a,c),(b,c),(a,d),(a,e),(b,d),(b,e),(c,d),(c,e)共9个,符合题意的基本事件为:(a,d),(a,e),(b,d),(b,e),(c,d),(c,e)共6个,因此,另一个为黄色的概率为:P=
知识点
在直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴建立极坐标系。已知曲线C1的极坐标方程为

(1)写出曲线C1与直线l的直角坐标方程;
(2)设Q为曲线C1上一动点,求Q点到直线l距离的最小值。
正确答案
见解析
解析
解析:
(1)

(2)设



当且仅当


知识点
已知椭圆







(1)当
(2)直线

正确答案
见解析
解析
解析:(1)由题意

于是圆心坐标为



即




所以



(2)假设相切, 则



故直线

知识点
已知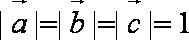
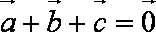
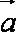
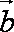
正确答案
解析
法1: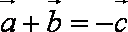
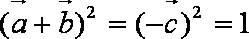
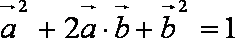
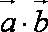
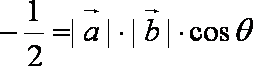
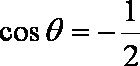
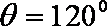
法2:由模都为1及向量的加法法则知,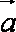
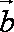
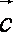
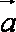
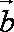
知识点
设函数
(1)判断函数f(x)在(0,+∞)上的单调性;
(2)证明:对任意正数a,存在正数x,使不等式f(x)-1<a成立。
请考生在22、23、24中任选一题作答.注意:只能做所选定的题目.如果多做,则按所做第一个题目计分,作答时请用2B铅笔在答题卡上将所选题号后的方框涂黑。
正确答案
见解析
解析
(1) 由题意知:
令h(x)=(x-1)ex+1,则h‘(x)=x ex>0,
∴h(x)在(0,+∞)上是增函数,
又h(0)=0,∴h(x)>0,则f’(x)>0,
∴f(x)在(0,+∞)上是单调增函数.
(2) 
令G(x)= ex-(a+1)x-1, G’(x)=ex-(a+1),
由G‘(x)=0得:x=ln(a+1),
当0<x< (ln(a+1)时,G’(x)<0,
当x>ln(a+1)时,G‘(x)>0,
∴当x=ln(a+1)时,G(x)min=a-(a+1)ln(a+1),
令

又
∴当a>0时,

即当x=ln(a+1)时,G(x)min=a-(a+1)ln(a+1)<0.
故存在正数x=ln(a+1),使不等式F(x)-1<a成立,
知识点
户外运动已经成为一种时尚运动,某单位为了了解员工喜欢户外运动是否与性别有关,对本单位的50名员工进行了问卷调查,得到了如下列联表:
已知在这50人中随机抽取1人抽到喜欢户外运动的员工的概率是
(1)请将上面的列联表补充完整;
(2)是否有99.5﹪的把握认为喜欢户外运动与性别有关?并说明你的理由;
(3)经进一步调查发现,在喜欢户外运动的10名女性员工中,有4人还喜欢瑜
伽.若从喜欢户外运动的10位女性员工中任选3人,记
的人数,求
下面的临界值表仅供参考:
(
正确答案
见解析。
解析
(1)



(2)


(3)




知识点
把函数


正确答案
解析
解:


再将图象向右平移


故选A。
知识点
已知函数
(1)当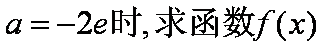
(2)若函数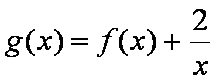
正确答案
见解析
解析
解析:
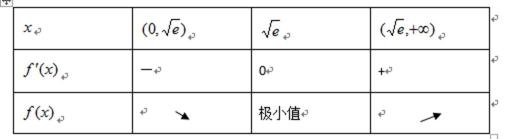
(1)函数
当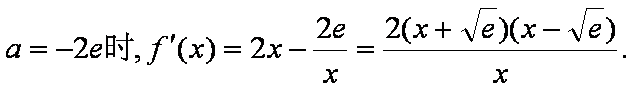
当x变化时,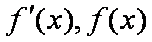
由上表可知,函数
单调递增区间是
极小值是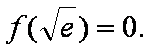
(2)由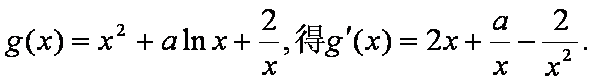
又函数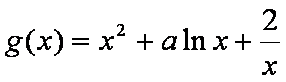
则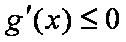
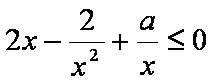
即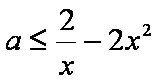
又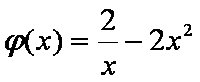
所以
所以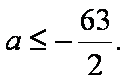
知识点
设函数
(1)当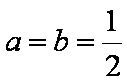
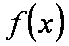
(2)令
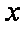
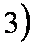
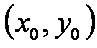
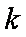
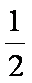

(3)当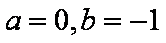
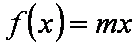
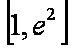
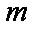
正确答案
(1)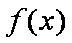
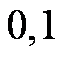

(2)
(3)
解析
(1)解:依题意,知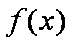
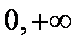
当 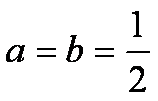
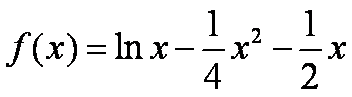
令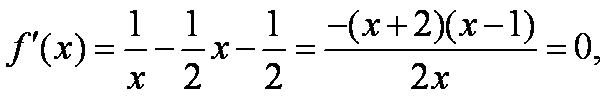
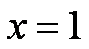
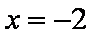
当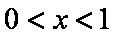
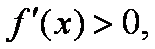
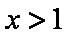
所以f(x)的单调增区间是(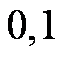

(2)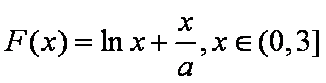
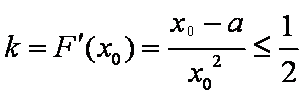
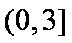
所以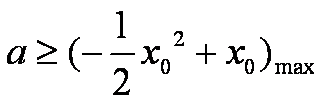
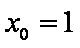
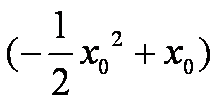
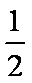
所以
(3)当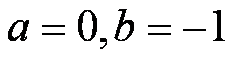
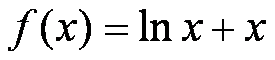
由
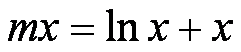
又因为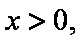
要是方程
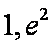

令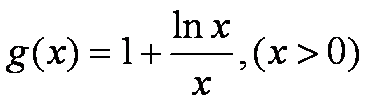
由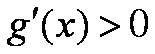
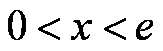
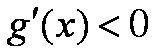
所以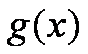

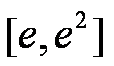
所以
所以
知识点
函数



正确答案
解析
利用换元法,将


当



可知当



故



知识点
扫码查看完整答案与解析