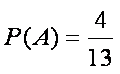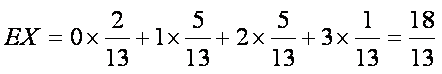- 导数与积分
- 共3028题
空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的指数,其数值越大说明空气污染状况越严重,对人体健康的危害也就越大。根据国家标准,指数在0-50之间时,空气质量为优;在51-100之间时,空气质量为良;在101-150之间时,空气质量为轻度污染;在151-200之间时,空气质量为中度污染;在大于200时,空气质量为重度污染。环保部门对某市5月1日至5月15日空气质量指数预报如下表:
某人选择5月1日至5月13日某一天到达该市,并停留三天.
(1)求此人到达当日空气重度污染的概率;
(2)设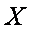
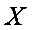
(3)根据上表判断从哪天开始连续三天的空气质量指数方差最大(不要求计算,只写出结果).
命题意图: 考查概率统计的基本运算及随机变量分布列,中档题。
正确答案
见解析。
解析
(1)记事件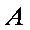
(2)此人在该市停留期间空气质量优良天数统计如下表:
所以随机变量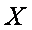
所以
(3)从5月3日开始连续三天的空气质量指数方差最大.
知识点
某中学篮球队进行投篮训练,每人在一轮练习中最多可投篮4次,且规定一旦投进即停止该轮练习,否则一直投到4次为止,已知队员甲每次投进的概率为
(1)求一轮练习中,队员甲的投篮次数


(2)在一轮练习中,队员甲至少投篮3次的概率。
正确答案
见解析
解析
解析:
(1)分布列为
期望为 
(2)
(2)向量法:
设



知识点
如图一个空间几何体的正视图、左视图、俯视图均为全等的等腰直角三角形,如果直角三角形的直角边长都为1,那么这个几何体的体积为 ( )
正确答案
解析
三视图所对应的空间几何体是一个三棱锥,其底面是边长为1的等腰直角三角形,三棱锥的高是1,故其体积是
知识点
已知函数
(1)若函数

(2)设直线







正确答案
见解析
解析
(1)

令



若
若


若
综上 若


若
(2)
设






设

当




且


知识点
在





(1)求
(2)若

正确答案
见解析。
解析
(1)由题意,
得
由于





(2)由

即

得


∴

知识点
已知数列





(1)求数列
(2)记



正确答案
见解析
解析
(1)由已知得
所以
(2)
当


当

①-②得
所以


(3)由(2)知,


所以当


所以

知识点
已知抛物线的顶点是坐标原点







(1)求抛物线的方程;
(2)在



(3)若





正确答案
(1)y2=4x
(2)m<-1
(3)[-6,-2]∪[2,6]
解析
(1)设抛物线方程


联立消去


设


所以

所求抛物线方程为
(2)因为



由(1)得



所以



所以


解得

(3)由条件可设


所以




根据抛物线定义可知,以




知识点
各项都是正数的等比数列



正确答案
解析
由题意







知识点
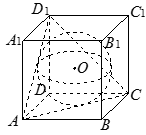
如图,在三棱锥









(1)求证:

(2)求

(3)设点





正确答案
见解析
解析
(1)因为 



所以 
又因为 

所以 

又因为 

所以 
因为 

所以 
又因为 
所以 

(2)在平面

因为 



由 




所以以








设平面



由 



设



所以 
即 
(3)因为 


又因为 

因为 



所以 
解得 
知识点
如图,已知球
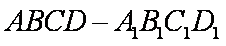
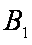
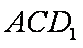

正确答案
解析


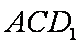
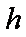

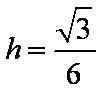
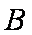
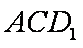
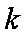
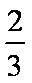
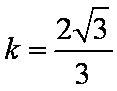
又球的半径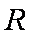
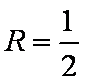
由勾股定理可知,截面圆的半径为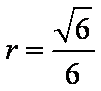
圆锥底面面积为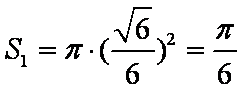
圆锥的母线可利用勾股定理求出: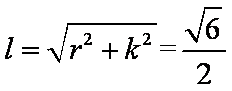
圆锥的侧面积为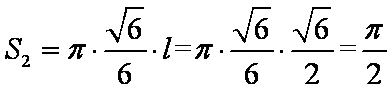
圆锥的表面积为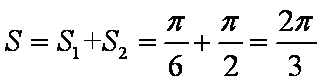
知识点
扫码查看完整答案与解析