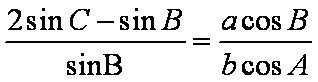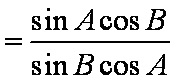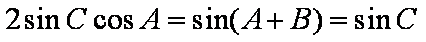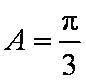- 导数与积分
- 共3028题
设


正确答案
解析
略
知识点
在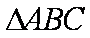
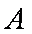
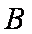

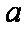
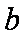
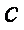
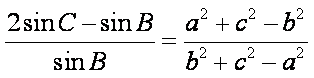
(1)求角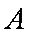
(2)若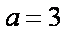
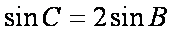
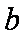
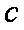
正确答案
见解析
解析
(1)由正弦定理得
所以
因为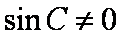
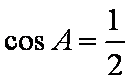
(2)由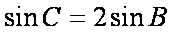
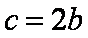
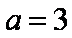
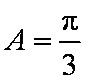
所以由余弦定理得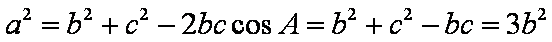
知识点
ΔABC的内角为A,B,C,若sinA=cosB=

正确答案
解析
∵






知识点
已知


(1)当

(2)若函数


正确答案
见解析。
解析
(1)
由
∴ 


(2)∵
∴
=
∵
∴

∵
即

∴
知识点
在复平面内,复数
正确答案
解析
略
知识点
如图所示,在四棱柱




(1)求证:
(2)若





正确答案
见解析
解析
方法一:(1)因为侧面

又
所以


(2)设线段














设



所以





由


设平面



得




又平面


故平面


方法二:(1)连接





连
由



所以



又根据菱形的性质


从而
(2)因为




延长





则






连接


由题意知


故


易知






故平面


知识点
设双曲线









正确答案
解析
略
知识点
已知函数
(1)当

(2)当函数

正确答案
见解析
解析
本题考查绝对值不等式解法、最值求解等基础知识,考查推理论证能力及运算求解能力。
(1)当

有不等式
当



当



当



综上函数

(2)∵函数


∴只要



即



知识点
函数f(x)=2sin(2x-φ)(|φ|<)的图像如图所示,则φ的值等于
正确答案
解析




故 
所以 
得


知识点
函数f(x)是定义域为{x|x≠0}的奇函数,且f(1)=1,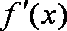
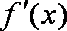

正确答案
解析
令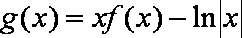
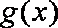
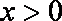
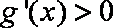
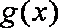
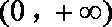
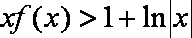
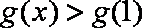
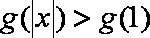
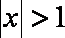
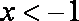
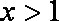
知识点
扫码查看完整答案与解析